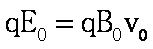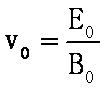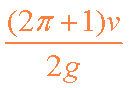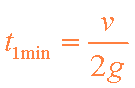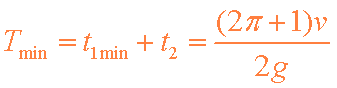- 磁场
- 共810题
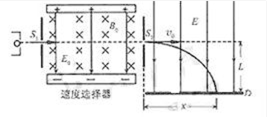
如图所示的装置,左半部为速度选择器,右半部为匀强的偏转电场。一束同位素离子流从狭缝
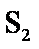
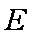
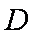
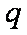
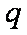
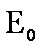
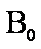
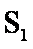

(1)求从狭缝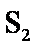
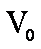
(2)若打在照相底片上的离子在偏转电场中沿速度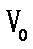
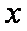
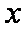

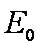
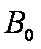
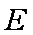
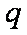
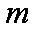
正确答案
见解析
解析
(1)能从速度选择器射出的的离子满足:
解得:
(2)离子进入匀强偏转电场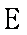
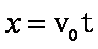
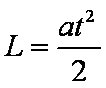
由牛顿第二定律得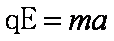
解得: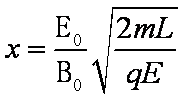
知识点
某仪器用电场和磁场来控制电子在材料表面上方的运动,如图所示,材料表面上方矩形区域PP′N′N充满竖直向下的匀强电场,宽为d;矩形区域NN′M′M充满垂直纸面向里的匀强磁场,磁感应强度为B,长为3s,宽为s;NN′为磁场与电场之间的薄隔离层,一个电荷量为e、质量为m、初速为零的电子,从P点开始被电场加速经隔离层垂直进入磁场,电子每次穿越隔离层,运动方向不变,其动能损失是每次穿越前动能的10%,最后电子仅能从磁场边界M′N′飞出,不计电子所受重力。
(1)求电子第二次与第一次圆周运动半径之比;
(2)求电场强度的取值范围;
(3)A是M′N′的中点,若要使电子在A、M′间垂直于AM′飞出,求电子在磁场区域中运动的时间。
正确答案
(1)0.9 (2)
解析
(1)设圆周运动的半径分别为R1、R2、…Rn、Rn+1…,第一和第二次圆周运动速率分别为v1和v2,动能分别为Ek1和Ek2.
由:Ek2=0.81Ek1,
得:R2∶R1=0.9
(2)设电场强度为E,第一次到达隔离层前的速率为v′。
由:
得:
又由:Rn=0.9n-1R1,
2R1(1+0.9+0.92+…+0.9n+…)>3s
得:
(3)设电子在匀强磁场中做圆周运动的周期为T,运动的半圆周个数为n,运动总时间为t.
由题意,有:
R1≤s,Rn+1=0.9nR1,Rn+1≥
得:n=2
又由:
得:
知识点
如图所示,将某正粒子放射源置于原点O,其向各方向射出的粒子速度大小均为v0、质量均为m、电荷量均为q。在0≤y≤d的一、二象限范围内分布着一个匀强电场,方向与y轴正向相同,在d<y≤2d的一、二象限范围内分布着一个匀强磁场,方向垂直于xoy平面向里。粒子离开电场上边缘y=d时,能够到达的最右侧的位置为(1.5d,d)。最终恰没有粒子从y=2d的边界离开磁场。已知sin37°=0.6,cos37°=0.8,不计粒子重力以及粒子间的相互作用,求:
17.电场强度E;
18.磁感应强度B;
19.粒子在磁场中运动的最长时间。
正确答案

解析
解析:(1)沿x轴正方向发射的粒子有x=1.5d,y=d
由类平抛运动基本规律得:


联立可得
考查方向
解题思路
(1)沿x轴正方向发射的粒子做类平抛运动,根据平抛运动基本公式列式求解E;
易错点
本题考查了带电粒子在电场和磁场中的运动,关键确定粒子运动的临界情况,通过几何关系解决,对学生数学几何能力要求较高
正确答案

解析
(2)沿x轴正方向发射的粒子射入磁场时有

联立可得

据题意知该粒子轨迹恰与上边缘相切,则其余粒子均达不到y=2d边界
由几何关系可知



考查方向
解题思路
(2)粒子沿x轴正方向射出的粒子进入磁场偏转的角度最大,若该粒子进入磁场不能打在ab板上,则所有粒子均不能打在ab板上.根据带电粒子在电场中类平抛运动,求出进入磁场中的偏转角度,结合几何关系得出轨道半径,从而得出磁感应强度的大小;
易错点
本题考查了带电粒子在电场和磁场中的运动,关键确定粒子运动的临界情况,通过几何关系解决,对学生数学几何能力要求较高
正确答案
;
解析

由几何关系可知圆心角

粒子运动周期

考查方向
解题思路
(3)粒子运动的最长时间对应最大的圆心角,经过(1.5d,d)恰与上边界相切的粒子轨迹对应的圆心角最大,根据几何关系结合周期公式求解.
易错点
本题考查了带电粒子在电场和磁场中的运动,关键确定粒子运动的临界情况,通过几何关系解决,对学生数学几何能力要求较高
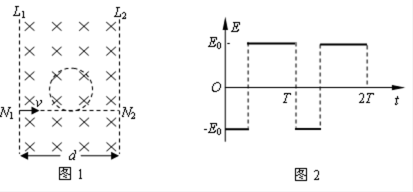
如图1所示,宽度为d的竖直狭长区域内(边界为L1、L2),存在垂直纸面向里的匀强磁场和竖直方向上的周期性变化的电场(如图2所示),电场强度的大小为E0,E>0表示电场方向竖直向上。t=0时,一带正电、质量为m的微粒从左边界上的N1点以水平速度v射入该区域,沿直线运动到Q点后,做一次完整的圆周运动,再沿直线运动到右边界上的N2点。Q为线段N1N2的中点,重力加速度为g。上述d、E0、m、v、g为已知量。
(1)求微粒所带电荷量q和磁感应强度B的大小;
(2)求电场变化的周期T;
(3)改变宽度d,使微粒仍能按上述运动过程通过相应宽度的区域,求T的最小值。
正确答案
(1)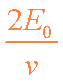
(2)
(3)
解析
(1)微粒做直线运动,则 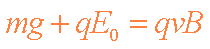
微粒做圆周运动,则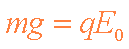
联立①②得: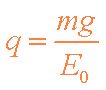
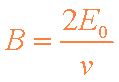
(2)设微粒从N1运动到Q的时间为t1,作圆周运动的周期为t2,则
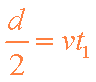

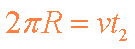
联立③④⑤⑥⑦得: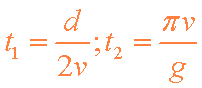
电场变化的周期 
(3)若微粒能完成题述的运动过程,要求 
联立③④⑥得:
设N1Q段直线运动的最短时间t1min,由⑤⑩11得
因t2不变,T的最小值
知识点
如图所示,二块水平放置.相距为d的长金属板接在电压可调的电源上。两板之间的右侧区域存在方向垂直纸面向里的匀强磁场。将喷墨打印机的喷口靠近上板下表面,从喷口连续不断喷出质量均为m.水平速度均为v0.带相等电荷量的墨滴。调节电源电压至U,墨滴在电场区域恰能沿水平向右做匀速直线运动,进入电场.磁场共存区域后,最终垂直打在下板的M点。
(1)判断墨滴所带电荷的种类,并求其电荷量;
(2)求磁感应强度B的值;
(3)现保持喷口方向不变,使其竖直下移到两板中间位置。为了使墨滴仍能到达下板M点应将磁感应强度调至B',则B'的大小为多少?
正确答案
见解析。
解析
(1) 墨滴在电场区域做匀速直线运动,有
得
由于电场方向向下,电荷所受电场力向上,可知:
墨滴带负电荷。
(2) 进入电场.磁场共存区域后,重力与电场力平衡,磁场力做匀速圆周运动的向心力,
考虑墨滴进入磁场和挡板的几何关系,可知墨滴在该区域恰完成四分之一圆周运动,则半径R=d,由此可得:
(3)根据题设,墨滴运动轨迹如图,设圆周运动半径为
由图示可得:
得:
知识点
有人设计了一种带电颗粒的速率分选装置,其原理如图所示,两带电金属板间有匀强电场,方向竖直向上,其中PQNM矩形区域内还有方向垂直纸面向外的匀强磁场,一束比荷(电荷量与质量之比)均为
求:
(1)电场强度E的大小;
(2)磁感应强度B的大小;
(3)速率为λv0(λ>1)的颗粒打在收集板上的位置到O点的距离。
正确答案
见解析。
解析
(1)设带电颗粒的电荷量为q,质量为m.有
Eq=mg
将
(2)如图,有
R2=(3d)2+(R-d)2
得
(3)如图所示,有
y2=ltanθ
y=y1+y2
得
知识点
如图所示,电源电动势








(1)当滑动变阻器接入电路的阻值为29欧时,电阻
(2)若小球进入板间做匀速度圆周运动并与板相碰,碰时速度与初速度的夹角为
正确答案
(1)0.6W
(2)54Ω
解析
(1)闭合电路的外电阻为

根据闭合电路的欧姆定律


R2两端的电压为

R2消耗的功率为

(2)小球进入电磁场做匀速圆周运动,说明重力和电场力等大反向,洛仑兹力提供向心力,
根据牛顿第二定律 

连立⑤⑥化简得

小球做匀速圆周运动的初末速的夹角等于圆心角为60°,根据几何关系得
R=d ⑧
连立⑦⑧带
干路电流为 

知识点
如图,与水平面成45°角的平面MN将空间分成I和II两个区域。一质量为m、电荷量为q(q>0)的粒子以速度v0从平面MN上的P0点水平向右射入I区。粒子在I区运动时,只受到大小不变、方向竖直向下的电场作用,电场强度大小为E;在II区运动时,只受到匀强磁场的作用,磁感应强度大小为B,方向垂直于纸面向里。求粒子首次从II区离开时到出发点P0的距离。粒子的重力可以忽略。
正确答案
带电粒子进入电场后,在电场力的作用下沿抛物线运动,其加速度方向竖直向下,设其大小为a,由牛顿定律得qE=ma①
设经过时间t0,粒子从平面MN上的点P1进入磁场,由运动学公式和几何关系得
v0t0=at02②
粒子速度大小V1为 V1=
设速度方向与竖直方向的夹角为α,则 tanα=
此时粒子到出发点P0的距离为 s0=
此后,粒子进入磁场,在洛仑兹力作用下做匀速圆周运动,圆周半径为 r1=
设粒子首次离开磁场的点为P2,弧P1P2所张的圆心角为2β,则P1到点P2的距离为
s1=2r1sinβ⑦
由几何关系得 α+β=45°⑧
联立①②③④⑤⑥⑦⑧式得 s1=
点P2与点P0相距 l=s0+s1⑩
联立①②⑤⑨⑩解得 l=
解析
略。
知识点
14.两相邻匀强磁场区域的磁感应强度大小不同、方向平行。一速度方向与磁感应强度方向垂直的带电粒子(不计重力),从较强磁场区域进入到较弱磁场区域后,粒子的( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.有两个匀强磁场区域I和 II,I中的磁感应强度是II中的k倍,两个速率相同的电子分别在两磁场区域做圆周运动。与I中运动的电子相比,II中的电子( )
A. 运动轨迹的半径是I中的k倍
B. 加速度的大小是I中的k倍
C. 做圆周运动的周期是I中的k倍
D. 做圆周运动的角速度与I中的相等
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析