- 函数的基本性质
- 共1471题
设a,b,m为整数(m>0),若a和b被m除得的余数相同,则称a和b对m同余,记为a=b(modm),已知


正确答案
解析
由题意,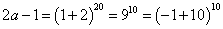

知识点
已知某篮球运动员2013年度参加了25场比赛,我从中抽取5场,用茎叶图统计该运动员5场中的得分如图1所示,则该样本的方差为
正确答案
解析
略
知识点
已知圆



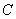

正确答案

解析
略
知识点
已知函数
(1)若


(2)求函数
(3)若


正确答案
(1)1
(2)

(3)
解析
(1)







当




所以

(2)令


当


由上表知


(3)要使




又


(ⅰ)当



解得 

(ⅱ) 当




解得
所以
(ⅲ)当



综上,

知识点
已知

正确答案
8
解析
略
知识点
设函数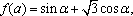


(1)若P点的坐标为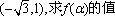
(2)若点



正确答案
见解析
解析
(1)由三角函数的定义,得
故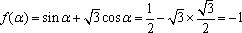
(2)
作出平面区域
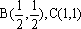

又

故当

当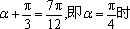
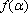

故函数

知识点
高为
正确答案
解析
知识点
如图,有一块锐角三角形的玻璃余料,欲加工成一个面积不小于

正确答案
解析
略
知识点
已知函数
(1)当

(2)当

(3)若存在


正确答案
见解析。
解析
知识点
曲线

正确答案
解析
略
知识点
扫码查看完整答案与解析


























