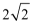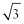- 二次函数的应用
- 共461题
20.已知椭




(1)若直线

(2)如果ΔBMN的重心恰好为椭圆的右焦点F,求直线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设集合A={1,2},则满足A∪B={1,2,3}的集合B的个数是( )
正确答案
解析
解:A={1,2},A∪B={1,2,3},
则集合B中必含有元素3,即此题可转化为求集合A={1,2}的子集个数问题,
所以满足题目条件的集合B共有22=4个.
故选择答案C.
知识点
9.某班3个男同学和3个女同学站成一排照相,要求任何相邻的两位同学性别不同,且男生甲和女生乙相邻,但甲和乙都不站在两端,则不同的站法种数是( )
正确答案
解析
解:根据题意,要求任何相邻的两位同学性别不同,男生与女生必须相间,
按甲所站的位置不同,分两种情况讨论,
①甲在男生的中间,其余的男生有2种站法,即男生共2种站法;
此时女生乙在女生中的站法有3种,若乙在左边或右边时,其余的女生2种站法,与男生有一种相间的方法,
若乙在中间,其余的女生2种站法,与男生有二种相间的方法,
则此时共2×(2×2×1+2×2)=16种;
②甲在男生的左边或右边时,其余的男生有2种站法,即男生共2种站法;
此生女生乙必须在女生的中间,其余的女生2种站法,与男生有二种相间的方法,
此时,共2×2×2=8种站法;
综合可得:共16+8=24种站法;
故选D.
知识点
14.已知数列



正确答案
4 , 5 , 32
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知

(Ⅰ)求
(Ⅱ)求函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知

(1)讨论

(2)求证:在(1)的条件下,
(3)是否存在实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知A、B两点分别在两条互相垂直的直线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.条件



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设曲线C:x2=y上有两个动点A、B,直线AB与曲线C在A点处切线垂直,则点B到y轴距离的最小值是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.在正方体上任选3个顶点连成三角形,则所得的三角形是直角非等腰三角形的概率为 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析