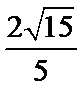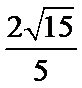- 空间两点间的距离公式
- 共8题
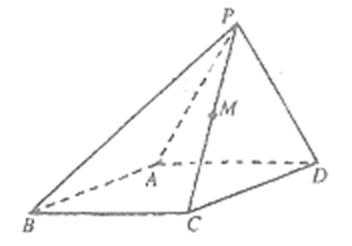
18.如图,在已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点E,连接PE并延长交AB于点G.
(I)证明G是AB的中点;
(II)在答题卡第(18)题图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
正确答案
(1)证明
∵ PD 

∵ DE

又∵ PD


∵ 正三棱锥P-ABC中PA=PB ∴ G为AB中点
(2)正三棱锥P-ABC中,PA=PB=PC ∵ 各侧面为直角三角形
∴PA



作EF//PB交PA于F 则EF
正三棱锥P-ABC中,D 为三角形ABC的重心,PA=6 ∴ AB=
∴DG=



∵ 


Rt

∴四面体PDEF体积
知识点
18.
如图,在已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点E,连接PE并延长交AB于点G.
(I)证明G是AB的中点;
(II)在答题卡第(18)题图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
正确答案
(1)证明:∵ PD

∵ DE

又∵ PD

∵ 正三棱锥P-ABC中PA=PB ∴ G为AB中点
(2) 正三棱锥P-ABC中,PA=PB=PC ∵ 各侧面为直角三角形
∴ PA


作EF//PB交PA于F 则EF
正三棱锥P-ABC中,D为三角形ABC的重心,PA=6 ∴ AB=6
∴ DG=


Rt△PGD中由射影定理PD=PE·PG ∴ PE=
∵ △PAB为等腰直角三角形,EF


∴ S△PAB=
Rt△PGD中 DE=

∴ 四面体PDEF体积 VD-PEF=

知识点
19.如图4所示,在矩形









(Ⅰ)求证:平面

(Ⅱ)若四棱锥


正确答案
(1)略;(2)
解析
.证明:(Ⅰ)∵


∴

故在四棱锥
又∵


∴

又



(Ⅱ)设


在等腰直角


由(Ⅰ)知

故
整理得

连结


于是
∵ 

设点F到



由
所以点F到平面

考查方向
解题思路
第(1)问先根据等腰证明


第(2)问先证明


易错点
无法找到线面垂直的条件;找不到

知识点
如图,四棱锥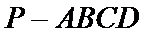
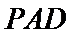
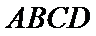
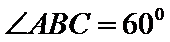
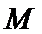
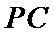
22.求证: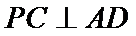
23.求点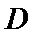
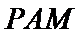
正确答案
(1)略;
解析
(1):取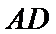
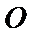
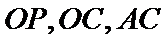
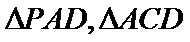
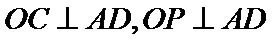
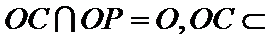
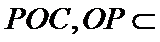
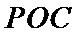
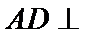
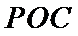
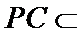
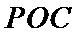
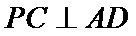
考查方向
解题思路
先证明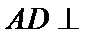
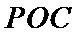
易错点
不会做辅助线导致没有思路;
正确答案
(2)
解析
(2)点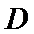
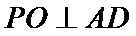
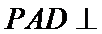
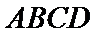

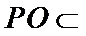
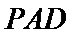
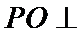
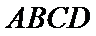
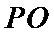
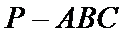
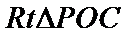
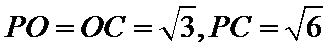
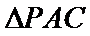
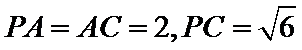
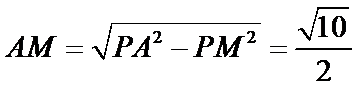
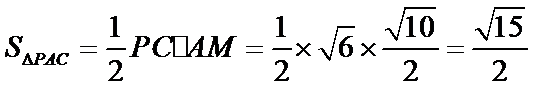
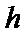
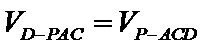
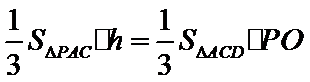
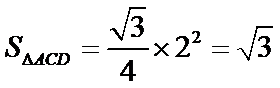
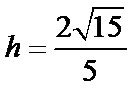
考查方向
解题思路
先发现点
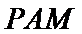
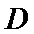
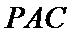
易错点
看不出点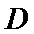
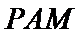
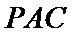
如图,在三棱柱




22.求证:

23.当三棱锥


正确答案
(略)
解析
连结















考查方向
解题思路
关键是在面DCB1中找线,连结


易错点
确定“三棱锥
正确答案
解析
设点








由(Ⅰ)知:




∵




∵




















考查方向
解题思路
当三棱锥





易错点
确定“三棱锥
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=BC=2,AD=CD=

(1)证明:BD⊥平面APC;
(2)若G为PC的中点,求DG与平面APC所成的角的正切值;
(3)若G满足PC⊥平面BGD,求
正确答案
见解析
解析
(1)设点O为AC,BD的交点。
由AB=BC,AD=CD,得BD是线段AC的中垂线。
所以O为AC的中点,BD⊥AC.
又因为PA⊥平面ABCD,BD
所以PA⊥BD.
所以BD⊥平面APC.
(2)连结OG.由(1)可知OD⊥平面APC,则DG在平面APC内的射影为OG,所以∠OGD是DG与平面APC所成的角。
由题意得OG=

在△ABC中,
AC=
=
所以OC=

在直角△OCD中,OD=
在直角△OGD中,tan∠OGD=
所以DG与平面APC所成的角的正切值为
(3)连结OG.因为PC⊥平面BGD,OG
在直角△PAC中,得PC=
所以GC=
从而PG=
所以
知识点
如图,弧
















(1)求异面直线

(2)将

正确答案
见解析
解析
(1)








(2)连结


由题设知,所得几何体为圆锥,其底面积为

该圆锥的体积为
知识点
如图6,在三棱锥







(1)求证:

(2)若



正确答案
见解析。
解析
(1)证明:在正



因为





又



所以
因为


又

所以

(2)解法1:设点


因为



因为

因为

所以
因为
由(1)知

在

所以
因为
所以
即
所以
故点


解法2:
过点



由(1)知,


所以

因为


因为


所以


因为



因为

因为


以下给出两种求
方法1:在△



则
因为
所以
方法2:在


在


所以
即
由①,②解得
故点


知识点
18.如图





(1)证明:

(2)证明:
(3)求点

正确答案
(1)由四边形



(2)先证



(3)取












试题解析:
(1)因为四边形






(2)因为四边形











(3)取































解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析