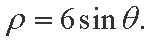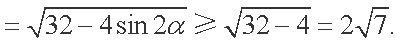- 直线和圆的方程
- 共1449题
已知集合
正确答案
解析
A=(-

知识点
设动点


正确答案
100
解析
略。
知识点
在区间
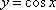
正确答案
3
解析
略
知识点
抽样统计甲、乙两位射击运动员的5次训练成绩(单位:环),结果如下:
则成绩较为稳定(方差较小)的那位运动员成绩的方差为__________。
正确答案
2
解析
由题中数据可得

于是



由
知识点
等差数列



正确答案
6
解析
可已知可得,
知识点
已知函数





(1) 

(3)(2013,0)是函数
(4)直线是函数
正确答案
解析
略
知识点
已知直线L:

正确答案
解析
略
知识点
在四棱锥










(1)求证:PA//平面BEF;
(2)若PC与AB所成角为

(3)在(2)的条件下,求二面角F-BE-A的余弦值。
正确答案
见解析
解析
(1)证明:连接AC交BE于O,并连接EC,FO









又 F为AD中点








(2)解法一:

易知 BCDE为正方形
建立如图空间直角坐标系


则

解得:

解法二:由BCDE为正方形可得
由ABCE为平行四边形 可得






(3)



设
则
取




由图可知二面角
所以二面角

知识点
全国十运会期间,某高校有14名志愿者参加接待工作,若每天排早、中、晚三班,每班4人,每人每天最多值一班,则开幕式当天不同的排班种数为 ( )
正确答案
解析
先从14人中选出12人,再将12人进行分组,且每组4人.
知识点
在直角坐标系xOy中,直线l的参数方程为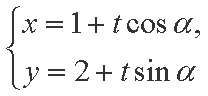
(1)求圆C的直角坐标方程;
(2)设圆C与直线l交于点A,B,若点P的坐标为(1,2),求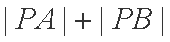
正确答案
见解析
解析
解析:(1)由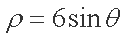
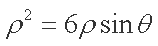
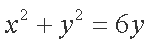
即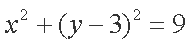
(2)将
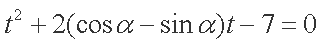
由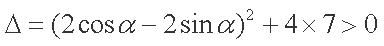
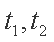
所以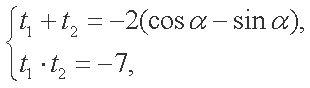

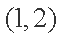
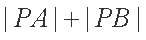
所以

知识点
3.设函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.用数字
正确答案
324
解析
解析已在路上飞奔,马上就到!
知识点
14. 已知函数


①函数

②函数

③若



④对任意


其中正确命题的序号是____________.(写出所有正确命题的编号)
正确答案
①③④
解析
解析已在路上飞奔,马上就到!
知识点
6.设



①若


②若




③若


④若





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析