- 函数的概念与基本初等函数
- 共5812题
3.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度




(1)当

(2)当车流密度

正确答案
(1)
(2)


解析
解析已在路上飞奔,马上就到!
知识点
19.定义在

①


②

③


(1)求函数
(2)设函数



正确答案
(1)
∵ 


∴
由

又


∴
由①②③得:

(2)由已知得:若存在

即存在

设
则
令

当



当



∴



而


于是有
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(1)求
(2)设




(3)当



正确答案
(1)
若



若

由
此时增区间为

当


当
(2)
设
若


同时



故

(3)结论:在区间


即证:当


设

有


解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数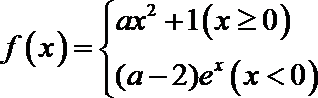
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在区间


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数的对称中心为







正确答案
-8046
解析
解析已在路上飞奔,马上就到!
知识点
9. 已知









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数


(1)




(2)求函数
(3)当



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析