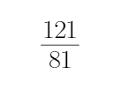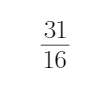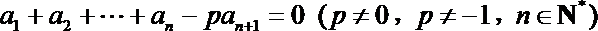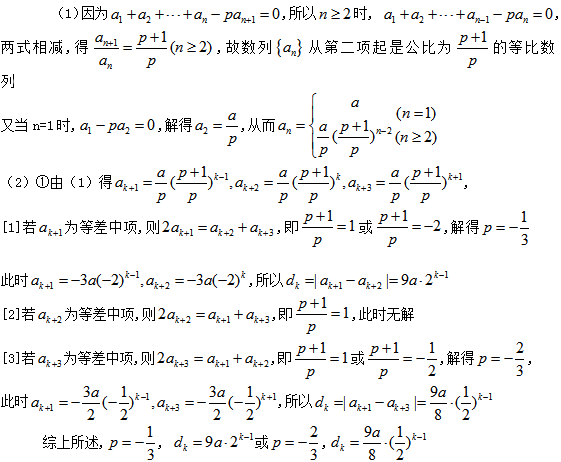- 等比数列
- 共414题
20. 已知数列





(1)求数列
(2)求证:
正确答案
(1)由

代入

整理,得
从而有




(2)




解析
解析已在路上飞奔,马上就到!
知识点
23.已知数列









(1)证明:
(2)设




(3)当

正确答案
(1)∵
∴

由


∵

即
(2)
当n≥2时,
∵
∴
∴

(3)由(1)知当

所以

显然最小项是前三项中的一项.
当




当




当

解析
解析已在路上飞奔,马上就到!
知识点
15.已知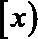

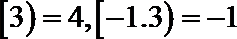
下列命题:
①函数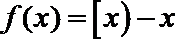
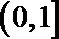
②若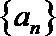
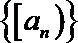
③若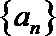
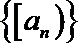
④若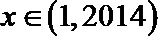
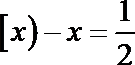
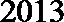
其中正确的的序号是____________.(把你认为正确的序号都填上)
正确答案
①④
解析
解析已在路上飞奔,马上就到!
知识点
17.在数列
(I)证明

(II)求

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知公比不为1的等比数列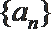
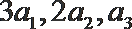

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列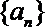
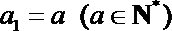
(1)求数列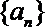
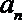
(2)若对每一个正整数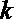
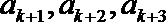
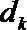
①求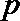
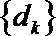
②记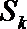
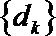
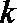
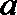
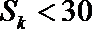

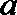
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列{



(Ⅰ)令


(Ⅱ)求数列

(Ⅲ)设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若数列




正确答案
解析
依题意可得bn+1=pbn,则数列

知识点
2.已知数列{an}中, a1=1,当n≥2时,an=2an-1+1,依次计算a2 , a3, a4后,猜想an的一个表达式是( ).
正确答案
解析
a2=2a1+1=2×1+1=3,
a3=2a2+1=2×3+1=7,
a4=2a3+1=2×7+1=15,
利用归纳推理,猜想an=2n-1,故选C
知识点
19.已知函数


(1)求证:数列
(2)令




正确答案
(1)证明:由题意得
又 ∵
∴
故数列{bn + 1}是以1为首项,2为公比的等比数列
(2) 由 (1)可知,
故
∴
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析