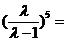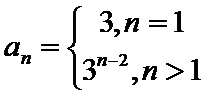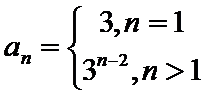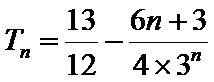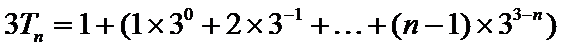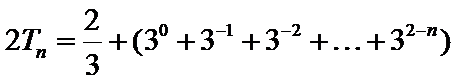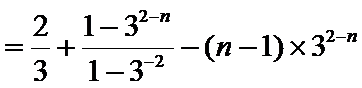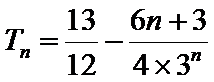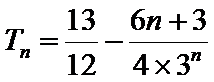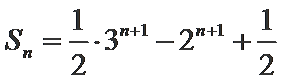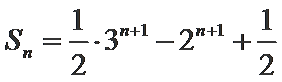- 等比数列
- 共414题
17.已知数列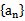
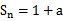
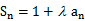
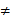
(I)证明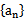
(II)若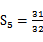
正确答案
见解析
解析
(Ⅰ)由题意得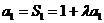
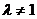
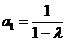
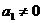
由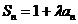
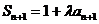
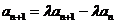
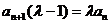
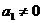
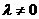
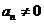
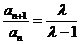
因此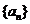
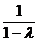
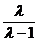
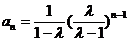
(Ⅱ)由(Ⅰ)得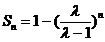
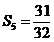
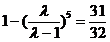
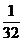
解得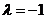
知识点
17.已知无穷等比数列





正确答案
解析



若

若

考查方向
解题思路
先将无穷等比数列前


易错点
对化简之后
知识点
20.设数列A:




(I)对数列A:-2,2,-1,1,3,写出G(A)的所有元素;
(I I)证明:若数列A中存在




(I I I)证明:若数列A满足



正确答案
知识点
设数列{an}的前n项和为Sn,已知2Sn=3n+3.
20.求{an}的通项公式;
21.若数列{bn},满足anbn=log3an,求{bn}的前n项和Tn.
正确答案
(1)
解析
(I)因为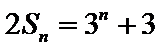
所以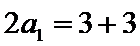
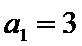
当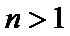
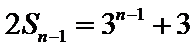
此时 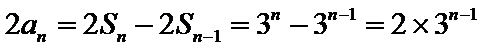
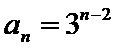
所以
考查方向
解题思路
运用从一般到特殊的处理方法,准确确定等差数列的通项公式。
(Ⅰ)利用2Sn=3n+3,可求得a1=3;当n>1时,2Sn﹣1=3n﹣1+3,两式相减2an=2Sn﹣2Sn﹣1,可求得an=3n﹣1,从而可得{an}的通项公式。
正确答案
(2)
解析
(II)因为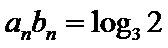
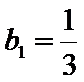
当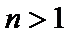
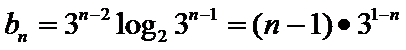
所以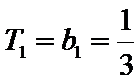
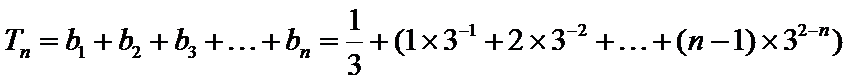
所以
两式相减,得
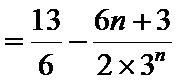
所以
经检验,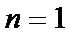
综上可得
考查方向
解题思路
(Ⅱ)依题意,anbn=log3an,可得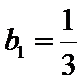
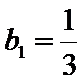
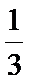
易错点
数列的错位相减求和时错项的处理,等差数列与等比数列的性质.
4.已知数列


正确答案
解析
因为
考查方向
解题思路
先写出前几项,然后找到规律,进而求解
易错点
找不出前n项和和数列通项的关系
知识点
2.设{an}是公比为q的等比数列,则“q>1”是“{an}为递增数列”的( )
正确答案
解析
根据指数函数的单调性,举反例:首项

考查方向
本题考查等比数列的单调性,充分条件与必要条件.
解题思路
等比数列的增减是由首项与公比确定的,当首项

易错点
对递增等比数列判断不准,对条件的性质判断不准.
知识点
11. 已知数列







正确答案
解析
设数列









考查方向
本题主要考查递推数列,数列与函数的关系,等差数列的定义等知识。
知识点
已知函数




(1)求证:数列
(2) 若




(3)若



正确答案
(1) 证:由题意
即
∴
∴
∵常数


∴数列


(2) 当


所以
因为

因而最小值为
(3) 由(1)知,


即

当



当




∵
∴当

∴

∴
综上所述,存在实数
解析
本题属于数列与不等式的综合应用题,题目的难度是偏难,本题的关键是:
(1)、利函数的性质求出数列的通项公式;
(2)、利用等比数列的求和公式求出前n项和的表达式,并求出最小值;
(3)、根据数学归纳法,分类讨论出k的取值范围。
考查方向
本题考查了数列的综合应用题,特别是数列与不等式之间的应用题
易错点
1、由


知识点
18.设数列{an}的前n项和为Sn,己知a1=l,nan+1=(n+2)Sn,n∈N*.
(1)求证:
(2)设Tn= S1+S2+--+Sn,求证:(n+l) Tn<nSn+1.
正确答案
(1)
(2)略.
解析
试题分析:本题属于数列中的基本问题,题目的难度是逐渐由易到难.
(1)由已知得
所以
(2)由上知


①-②得:
即(n+l) Tn<nSn+1.
考查方向
本题考查了数列的问题.属于高考中的高频考点。
解题思路
本题考查数列问题,解题步骤如下:
(1)利用等比数列的定义证明。
(2)利用错位相减法求和。
易错点
错位相减法求和时相减的结果项数易错。
知识点
20.设数列{an}满足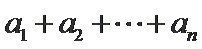
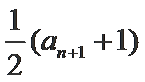
(1)求证数列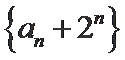
(2)求数列{an}的前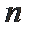
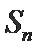
正确答案
(1)略
(2)
解析
(1) 解 由条件可得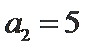
两式相减整理得an+1-3an=2n,则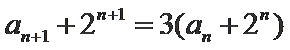
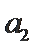
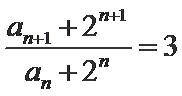
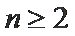
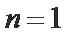
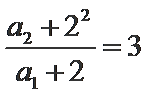
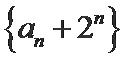
(2)法一:由2Sn=an+1-2n+1+1直接可得
法二:直接求和公式.
考查方向
本题主要考查等比数列的定义以及与之间的关系等知识。
解题思路
利用等式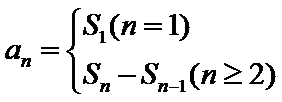
易错点
第一问没有验证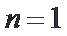
知识点
扫码查看完整答案与解析