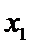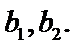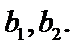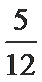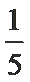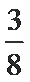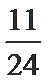- 概率与统计
- 共1631题
某商场根据以往某种商品的销售记录,绘制了日销售量的频率分布表(如表)和频率分布直方图(如图).
将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
18.求
19.求在未来连续3天里,有连续2天的日销售量都高于100个且另1天的日销售量不高于50个的概率;
正确答案



解析
解:由频率分布直方图,得:



考查方向
解题思路
本题主要考查了统计、独立事件的概率及二项分布的应用,解题步骤如下:由频率算出频率/组距的值再作出对应的图。
易错点
审题不清和考虑不全面导致出错。
正确答案
0.108
∴EX=3×0.6=1.8
解析
解:设A1表示事件“日销售量高于100个”,A2表示事件“日销售量不高于50个”,B表示事件“在未来连续3天里有连续2天日销售量高于10
故所求概率:P(B)=0.6×0.6×0.15×2=0.108.
20.用X表示在未来3天里日销售量高于100个的天数,求随机变量X的分布列和数学期望.
解:依题意,X的可能取值为0,1,2,3,且X~B(3,0.6).
P(X=0)=
P(X=2)=
∴X的分布列为
∴EX=3×0.6=1.8.
考查方向
解题思路
本题主要考查了统计、独立事件的概率及二项分布的应用,解题步骤如下:
根据题设求出相应概率。
本题主要考查了统计、独立事件的概率及二项分布的应用,解题步骤如下:分析
易错点
审题不清和考虑不全面导致出错。
审题不清和考虑不全面导致出错。
有编号为
其中难度系数小于0.50的为难题.
18.从上述9道题中,随机抽取1道,求这道题为难题的概率;
19.从难题中随机抽取2道,求这两道题目难度系数相等的概率.
正确答案
解析
记“从9道题中,随机抽取1道为难题”为事件




考查方向
解题思路
列举出全部事件、基本事件所包含的个数,容易得出结论。
易错点
本题易在列举基本事件包含的个数时发生错误。
正确答案
解析
【解析】记“从难题中随机抽取2道难度系数相等”为事件








考查方向
解题思路
列举出全部事件、基本事件所包含的个数,容易得出结论。
易错点
本题易在列举基本事件包含的个数时发生错误。
9.已知一次函数





正确答案
解析
f(0)=-1;f(1)=a-1, 使得



考查方向
解题思路
由于是直线型函数,求两个端点值,f(1)=a-1<0,解得 a
易错点
对于恒成立问题理解错,数形结合应用。
知识点
以下茎叶图记录了甲、乙两组各四名同学的植树棵树,乙组记录中有一个数据模糊,无法确认,在图中以X表示。
19.如果X=8,求乙组同学植树棵树的平均数和方差。
20.如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵树Y的分布列和数学期望。
正确答案
解析
当X=8时,由茎叶图可知,乙组同学的植树棵数是:8,8,9,10。………2
所以平均数为
方差为
考查方向
解题思路
按题意直接求平均,按公式直接求方差
易错点
第(2)问随机变量找不准,对应有概率计算不准确。
正确答案
随机变量Y的分布列为:
数学期望19
解析
当X=9时,由茎叶图可知,甲组同学的植树棵树是:9,9,11,11;
乙组同学的植树棵数是:9,8,9,10。
分别从甲、乙两组中随机选取一名同学,共有4×4=16种可能的结果,
这两名同学植树总棵数Y的可能取值为17,18,19,20,21。
事件“Y=17”等价于“甲组选出的同学植树9棵,乙组选出的同学植树8棵”,
所以该事件有2种可能的结果,
因此P(Y=17)=
同理可得P(Y=18)=



所以,随机变量Y的分布列为:
EY=17×




考查方向
解题思路
统计事件总为4×4=16,总棵数Y的可能取值为17,18,19,20,21。算出概率,列分布列,直接求数学期望
易错点
第(2)问随机变量找不准,对应有概率计算不准确。
周立波是海派清口创始人和《壹周·立波秀》节目的主持人,他的点评视角独特,语言幽默犀利,给观众留下了深刻的印象.某机构为了了解观众对《壹周·立波秀》节目的喜爱程度,随机调查了观看了该节目的140名观众,得到如下的列联表:(单位:名)
19.从这60名男观众中按对《壹周·立波秀》节目是否喜爱采取分层抽样,抽取一个容量为6的样本,问样本中喜爱与不喜爱的观众各有多少名?
20,根据以上列联表,问能否在犯错误的概率不超过0.025的前提下认为观众性别与喜爱《壹周·立波秀》节目有关.(精确到0.001)
21.从19题中的6名男性观众中随机选取两名作跟踪调查,求选到的两名观众都喜爱《壹周·立波秀》节目的概率.
正确答案
喜爱的观众有4名;不喜爱的观众有2名.
解析
抽样比为

考查方向
解题思路
直接计算抽样比,即可算出喜爱与不喜爱的人数;
易错点
对“独立性检验的思想”不理解易出错
正确答案
不能在犯错误的概率不超过0.025的前提下认为观众性别与喜爱有关.
解析
假设:观众性别与喜爱无关,由已知数据可求得,
∴ 不能在犯错误的概率不超过0.025的前提下认为观众性别与喜爱有关.
考查方向
解题思路
直接代入公式计算
易错点
对“独立性检验的思想”不理解易出错
正确答案
0.4
解析
记喜爱的4名男性观众为a,b,c,d,不喜爱的2名男性观众为1
其中选到的两名观众都喜爱的事件有6个,
故其概率为
考查方向
解题思路
直接列出总事件及发生事件的情况,直接求比。
易错点
对“独立性检验的思想”不理解易出错
13.甲、乙两人在5次综合测评中成绩的茎叶图如图所示,其中一个数字被污损,记甲,乙的平均成绩分别为


正确答案
解析
由已知题中的茎叶图,可得乙的5次综合测评中的成绩分别为87,86,92,94,91,则乙的平均成绩:






=





考查方向
解题思路
先设污损数字为



易错点
本题易在求被污损数字的范围时发生错误 。
知识点
13.甲、乙两人在5次综合测评中成绩的茎叶图如图所示,其中一个数字被污损,记甲,乙的平均成绩分别为


正确答案
解析
由已知题中的茎叶图,可得乙的5次综合测评中的成绩分别为87,86,92,94,91,则乙的平均成绩:












考查方向
解题思路
先设污损数字为



易错点
本题易在求被污损数字的范围时发生错误 。
知识点
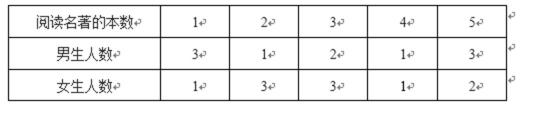
为了解学生暑假阅读名著的情况,一名教师对某班级的所有学生进行了调查,调查结果如下表.
17.从这班学生中任选一名男生,一名女生,求这两名学生阅读名著本数之和为4
的概率?
18.若从阅读名著不少于4本的学生中任选4人,设选到的男学生人数为
量
19.试判断男学生阅读名著本数的方差

写出结论).
正确答案

解析
试题分析:本题属常见的概率问题,在审题时一要会识表,二要从题意中提炼数据列分布列计算概率和期望即可。其难度和其它概率问题一样难度适中,主要是题意的理解。
设事件
读本数之和为4 .
由题意可知, 
考查方向
解题思路
本题考查概率和期望的计算,解题步骤如下:
从频数分布表读出数据再分析完成第一问得出结论。
找X,计算概率,列分布列,再计算期望。
易错点
第一问由频数分布表得出数据时易出错。第二、三问分布列中概率计算上易出错,再就是期望的计算也是学生易错点之一。
正确答案
EX=2;
解析
试题分析:本题属常见的概率问题,在审题时一要会识表,二要从题意中提炼数据列分布列计算概率和期望即可。其难度和其它概率问题一样难度适中,主要是题意的理解。
阅读名著不少于4本的学生共8人,其中男学生人数为4人,故

由题意可得




所以随机变量
随机变量

考查方向
解题思路
本题考查概率和期望的计算,解题步骤如下:
从频数分布表读出数据再分析完成第一问得出结论。
找X,计算概率,列分布列,再计算期望。
易错点
第一问由频数分布表得出数据时易出错。第二、三问分布列中概率计算上易出错,再就是期望的计算也是学生易错点之一。
正确答案

解析
试题分析:本题属常见的概率问题,在审题时一要会识表,二要从题意中提炼数据列分布列计算概率和期望即可。其难度和其它概率问题一样难度适中,主要是题意的理解。
(Ⅲ)
考查方向
解题思路
本题考查概率和期望的计算,解题步骤如下:
从频数分布表读出数据再分析完成第一问得出结论。
找X,计算概率,列分布列,再计算期望。
易错点
第一问由频数分布表得出数据时易出错。第二、三问分布列中概率计算上易出错,再就是期望的计算也是学生易错点之一。
某班倡议假期每位学生至少阅读一本名著,为了解学生的阅读情况,对该班所有学生进行了调查.调查结果如下:
19.试根据上述数据,求这个班级女生阅读名著的平均本数;
20.若从阅读5本名著的学生中任选2人交流读书心得,求选到男生和女生各1人的概率;
21.试判断该班男生阅读名著本数的方差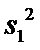
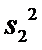

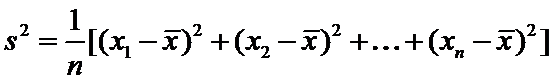
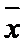
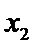
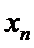
正确答案
3本;
解析
试题分析:本题属常见的统计类问题,在审题时一要会识图,二要认真列出基本事件再下手去做。题目较简单,主要是题意的理解。
(Ⅰ)女生阅读名著的平均本数
考查方向
解题思路
本题考查统计的相关知识和概率的计算,解题步骤如下:
由频数分布表分析数据,求出平均数即可。
根据题意列出基本事件完成概率的计算,再根据方差的计算公式完成第三问。
易错点
此题难度不大,主要是题意的理解,数据的计算,属于送分题。
正确答案
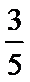
解析
试题分析:本题属常见的统计类问题,在审题时一要会识图,二要认真列出基本事件再下手去做。题目较简单,主要是题意的理解。
(Ⅱ)设事件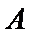
男生阅读5本名著的3人分别记为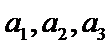
从阅读5本名著的5名学生中任取2人,共有10个结果,分别是:
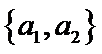
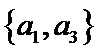
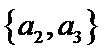
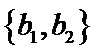
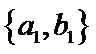
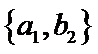
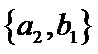
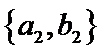
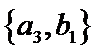
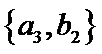
其中男生和女生各1人共有6个结果,分别是:
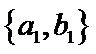
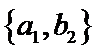
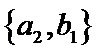
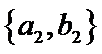
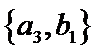
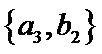
则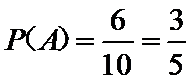
考查方向
解题思路
本题考查统计的相关知识和概率的计算,解题步骤如下:
由频数分布表分析数据,求出平均数即可。
根据题意列出基本事件完成概率的计算,再根据方差的计算公式完成第三问。
易错点
此题难度不大,主要是题意的理解,数据的计算,属于送分题。
正确答案
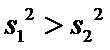
解析
试题分析:本题属常见的统计类问题,在审题时一要会识图,二要认真列出基本事件再下手去做。题目较简单,主要是题意的理解。
(Ⅱ)设事件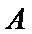
男生阅读5本名著的3人分别记为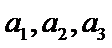
从阅读5本名著的5名学生中任取2人,共有10个结果,分别是:
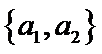
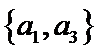
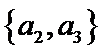
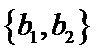
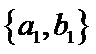
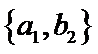
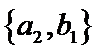
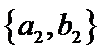
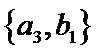
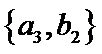
其中男生和女生各1人共有6个结果,分别是:
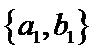
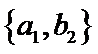
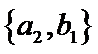
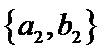
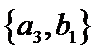
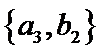
则
(Ⅲ)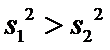
考查方向
解题思路
本题考查统计的相关知识和概率的计算,解题步骤如下:
由频数分布表分析数据,求出平均数即可。
根据题意列出基本事件完成概率的计算,再根据方差的计算公式完成第三问。
易错点
此题难度不大,主要是题意的理解,数据的计算,属于送分题。
某汽车公司为了考查某4S店的服务态度,对到店维修保养的客户进行回访调查,每个用户在到此店维修或保养后可以对该店进行打分,最高分为10分.上个月公司对该4S店的100位到店维修保养的客户进行了调查,将打分的客户按所打分值分成以下几组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10],得到频率分布直方图如图所示.
19.分别求第四、五组的频率;
20.该公司在第二、三组客户中按分层抽样的方法抽取6名客户进行深入调查,之
后将从这6人中随机抽取2人进行物质奖励,求得到奖励的人来自不同组的概率.
正确答案
第四、五组的频率分别为
解析
由直方图知,第四组的频率为



考查方向
解题思路
求出四、五组的矩形面积即为频率;列举法求解古典概型.
易错点
频率分布直方图的纵轴表示的是频率/組距;古典概型的解题步骤规范性.
正确答案

解析
(1)由直方图知,第四组的频率为



(2) 由直方图知,第二、三组客户人数分别为10人和20人,所以抽出的6人中,第二组有2人,设为A,B,第三组有4人,设为a,b,c,d.
从中随机抽取2人的所有情况如下:
AB,Aa,Ab,Ac,Ad,Ba,Bb,Bc,Bd,ab,ac,ad,bc,bd,cd共15种.…8分
其中,两人来自不同组的情况共有8种, 分别是Aa,Ab,Ac,Ad,Ba,Bb,Bc,Bd,…10分
所以,得到奖励的人来自不同组的概率为
考查方向
解题思路
求出四、五组的矩形面积即为频率;列举法求解古典概型.
易错点
频率分布直方图的纵轴表示的是频率/組距;古典概型的解题步骤规范性.
4.口袋
正确答案
解析
记取到的两个球都是白球为事件A, 取到的两个球同色为事件B
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
利用
易错点
在利用公式计算条件概率时,在条件发生的前提下,样本容量已经发生改变。
知识点
18. 现有甲、乙两个靶,某射手向甲靶射击一次,命中的概率为

(Ⅰ)求该射手恰好命中一次的概率;
(Ⅱ)求该射手的总得分

正确答案
见解析
知识点
公安机关服从中国共产党的领导,必须是( )。
A.相对的
B.无条件的
C.全面的
D.间接的
正确答案
B,C
解析
[解析] 公安机关服从中国共产党的领导,必须是绝对的、无条件的、全面的和直接的。故选BC。
10.设区域




正确答案
解析
如图所示区域,对应的部分是变长为1的正方形,区域A对应部分为图中阴影部分,面积为:
所以由几何概型可知概率为
考查方向
几何概型
解题思路
首先利用定积分求出阴影部分区域面积,然后利用定积分求几何概型概率
易错点
作图错误,定积分求错
知识点
5.有6人入住某家庭旅馆的6个不同房间,其中的一楼有两个房间,二楼有两个房间,三楼有两个房间,若每人随机地入住这6个房间中的一个房间,则其中的甲乙两人恰好在同一楼层的两个房间的概率为( )
正确答案
解析
只考虑甲乙两人,总的方法种数为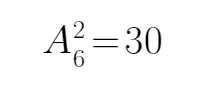
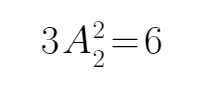
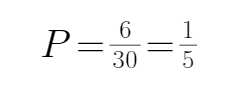
考查方向
随机事件发生的概率
列举法求概率
解题思路
只考虑甲乙两人,可得总的方法种数为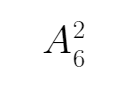
易错点
计算错误,分析情况时有重漏
教师点评
本题考查古典概型及其概率公式,属高考常考基础题
知识点
扫码查看完整答案与解析