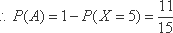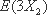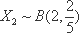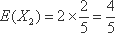- 概率与统计
- 共1631题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
从0,1,2,3,4,5,6,7,8,9中任取七个不同的数,则这七个数的中位数是6的概率为 。
正确答案
解析
6之前6个数中取3个,6之后3个数中取3个,
知识点
随机抽取9个同学中,至少有2个同学在同一月出生的概率是 (默认每月天数相同,结果精确到
正确答案
0.985
解析
9位同学生日月份的可能有

故至少有2个同学在同一月出生的概率为

知识点
将一枚均匀的硬币投掷6次,则正面出现的次数比反面出现的次数多的概率为
正确答案
解析
硬币投掷6次,有三类情况,①正面次数比反面次数多;②反面次数比正面次数多;③正面次数而后反面次数一样多;,③概率为
知识点
从个位数与十位数之和为奇数的两位数中任取一个,其中个位数为
正确答案
解析
首先求“个位数与十位数之和为奇数的两位数”的个数,利用“奇数+偶数=奇数”分两种情况求:①即十位数字分别为1,3,5,7,9时,个位数字可以为:0,2,4,6,8,此时有





知识点
设


(1)记使得“

(2)设


正确答案
见解析。
解析
(1)由


由于整数


(2)由于



且有



故
所以

知识点
风险是指资产收益率的不确定性,通常可以用( )进行衡量。
A.必要收益率
B.算术平均数
C.方差
D.标准差
E.期望收益率
正确答案
C,D
解析
[解析] 风险是指资产收益率的不确定性,通常可以用方差和标准差进行衡量。
贵阳市某中学高三(2)班排球队和篮球队各有10名同学,现测得排球队10人的身高(单位:cm)分别是:162,170,171,182,163,158,179,168,183,168,篮球队10人的身高(单位:cm)分别是:170,159,162,173,181,165,176,168,178,179.
19.请把两队身高数据记录在图中所示的茎叶图中,并求出两个队的身高的平均数;
20.现从两队所在身高超过178cm的同学中随机抽取三名同学,则恰好两人来自排球队一人来自篮球队的概率是多少?
正确答案
(Ⅰ)画出茎叶图如图2.
图2
…………………………………………………………………(2分)



解析
(Ⅰ)画出茎叶图如图2.
图2
…………………………………………………………………(2分)


考查方向
主要考茎叶图和平均数的计算。
解题思路
根据茎叶图的定义画出茎叶图,根据公式计算平均数。
易错点
公式记错,算平均数时计算错误。
教师点评
此题着手点低,代入公式即可解决问题。
正确答案
(Ⅱ)两队所有身高超过178cm的学生共有5人,
其中3人来自排球队记为a,b,c,2人来自篮球队记为A,B,
则从5人中抽取3名学生的基本事件

其中恰好2人来自排球队1人来自篮球队的事件为{a,b,A},{a,b,B},{a,c,A},{a,c,B},{b,c,A},{b,c,B},共6个,
∴恰好2人来自排球队1人来自篮球队的概率
解析
(Ⅱ)两队所有身高超过178cm的学生共有5人,
其中3人来自排球队记为a,b,c,2人来自篮球队记为A,B,
则从5人中抽取3名学生的基本事件

其中恰好2人来自排球队1人来自篮球队的事件为{a,b,A},{a,b,B},{a,c,A},{a,c,B},{b,c,A},{b,c,B},共6个,
∴恰好2人来自排球队1人来自篮球队的概率
考查方向
本题主要考查简单随机抽样的概率问题。
解题思路
应用简单随机抽样的方法,一一列举出来,便解决问题。
易错点
在写随机事件的中数的时候容易漏写或多写。
教师点评
本题主要考查了随机事件的概率问题及简单的随机抽样。
抛物线
正确答案
解析
正确答案
考查方向
坐标
解题思路
熟悉抛物线的曲线样式
易错点
注意与双曲线的区别
知识点
某购物网站在2013年11月开展“全场6折”促销活动,在11日当天购物还可以再享受“每张订单金额(6折后)满300元时可减免100元”.某人在11日当天欲购入原价48元(单价)的商品共42件,为使花钱总数最少,他最少需要下的订单张数为()
正确答案
解析
略
知识点
有甲、乙两个篮球运动员,每人各投篮三次,甲三次投篮命中率均为

如果又未中,则乙进行第三次投篮,并且在投篮时距离为16米,乙若投中,则不再继续
投篮,且知乙命中的概率与距离的平方成反比。
(1)求乙投篮命中的概率;
(2)求甲三次投篮命中次数ξ的期望与方差,
正确答案
见解析。
解析
(1)记乙三次投篮依次为事件A、B、C,设乙命中概率与距离的平方成反比的比例系
数为a,则由题意得:

故乙投篮命中的概率为

(2)甲重复三次投篮的命中次数ξ服从二项分布,即
则
知识点
袋中装有大小和形状相同的小球若干个黑球和白球,且黑球和白球的个数比为4:3,从中任取2个球都是白球的概率为

(1)求袋中原有白球、黑球的个数;
(2)求随机变量
正确答案
见解析。
解析
(1)依题意设袋中原有

由题意知
即

即袋中原有3个白球和4个黑球.
(2)依题意,



同理可得,

知识点
在一场娱乐晚会上,有5位民间歌手(1至5号)登台演唱,由现场数百名观众投票选出最受欢迎歌手,各位观众须彼此独立地在选票上选3名歌手,其中观众甲是1号歌手的歌迷,他必选1号,不选2号,另在3至5号中随机选2名,观众乙和丙对5位歌手的演唱没有偏爱,因此在1至5号中随机选3名歌手。
(1)求观众甲选中3号歌手且观众乙未选中3号歌手的概率;
(2)X表示3号歌手得到观众甲、乙、丙的票数之和,求X的分布列及数学期望。
正确答案
(1) 
解析
(1)设A表示事件“观众甲选中3号歌手”,B表示事件“观众乙选中3号歌手”,
则P(A)=

∵事件A与B相互独立,
∴观众甲选中3号歌手且观众乙未选中3号歌手的概率为P(A


(2)设C表示事件“观众丙选中3号歌手”,则P(C)=
∵X可能的取值为0,1,2,3,且取这些值的概率分别为
P(X=0)=
P(X=1)=
=
P(X=2)=P(AB



P(X=3)=P(ABC)=
∴X的分布列为
∴X的数学期望
知识点
某联欢晚会举行抽奖活动,举办方设置了甲,乙两种抽奖方案,方案甲的中奖率为

(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为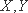

(2)若小明,小红两人都选择方案甲或方案乙进行抽奖,问:他们选择何种方案抽奖,累计的得分的数学期望较大?
正确答案
见解析
解析
(1)由已知得:小明中奖的概率为

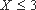
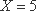
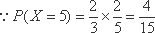

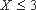
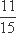
(2)设小明,小红都选择方案甲抽奖中奖的次数为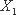
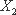
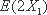
由已知: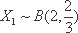
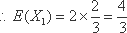
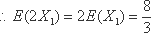

知识点
扫码查看完整答案与解析