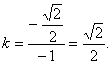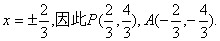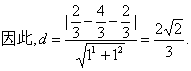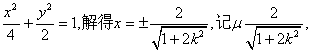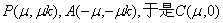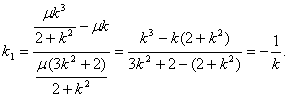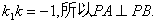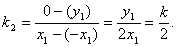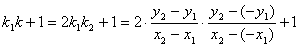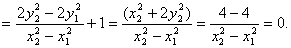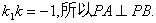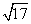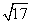- 三角函数的概念、同角三角函数的关系式和诱导公式
- 共714题
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知函数
（1）证明：
（2）求不等式
正确答案
见解析
解析
（1）
当
所以
（2）由（1）可知，
当
当
当
综上，不等式
知识点
下列函数中，既是偶函数又在区间(－∞，0)上单调递增的是( )
A
Bf(x)＝x2＋1
Cf(x)＝x3
Df(x)＝2－x
正确答案
解析
由偶函数的定义知，A，B为偶函数。A选项，
知识点
若变量x，y满足约束条件
正确答案
7
解析
不等式组表示的平面区域如图阴影部分所示，
作直线l0：2x＋y＝0并平移，当直线经过点A(3,1)时，在y轴上的截距最大，此时z取得最大值，且最大值为7.
知识点
在△ABC中，∠A＝90°，AB＝1，AC＝2，设点P，Q满足
A
B
C
D2
正确答案
解析
设
∴|a|＝1，|b|＝2，且a·b＝0。
＝［(1－λ)b－a］·(λa－b)
＝－λa2－(1－λ)b2＝－λ－4(1－λ)＝3λ－4＝－2，∴
知识点
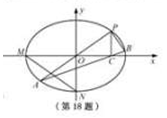
如图，在平面直角坐标系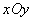
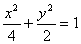
（1）当直线PA平分线段MN，求k的值；
（2）当k=2时，求点P到直线AB的距离d；
（3）对任意k>0，求证：PA⊥PB
正确答案
见解析
解析
（1）由题设知，
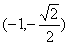
（2）直线PA的方程
解得
于是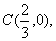
（3）解法一：
将直线PA的方程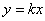
则
故直线AB的斜率为
其方程为
解得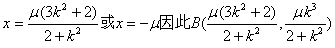
于是直线PB的斜率
因此
解法二：
设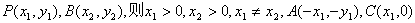
设直线PB，AB的斜率分别为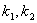
从而
因此
知识点
从正方形四个顶点及其中心这5个点中任取2个点，则这2个点的距离小于该正方形边长的概率为（ ）
A
B
C
D
正确答案
解析
设正方形边长为1，则从正方形四个顶点及其中心这5个点中任取2个点，共有10条线段，4条长度为1，4条长度为
∴所求概率为
知识点
一个空间几何体的三视图如图所示，则该几何体的表面积为
A48
B32+8
C48+8
D80
正确答案
解析
略
知识点
设圆
正确答案
解析
依题意得，
知识点
设a＋b＝2，b＞0，则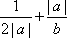
正确答案
解析
因为a＋b＝2，
所以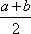
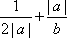
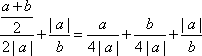
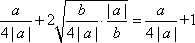
当a＞0时，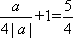
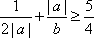
当a＜0时，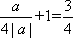
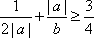
综上可得最小值为
知识点
扫码查看完整答案与解析