- 导数的运算
- 共219题
函数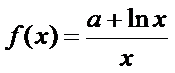

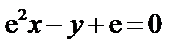
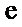

25.若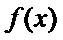
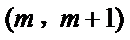


26.求证:当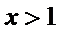
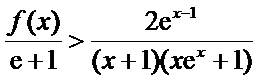
正确答案
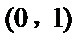
解析
因为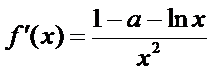
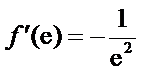
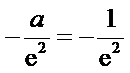
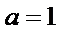
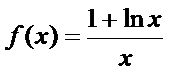
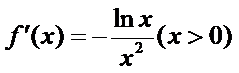
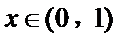
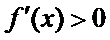
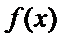
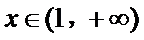
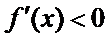
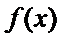
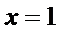
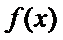
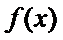
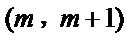
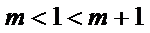
即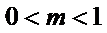
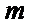
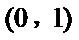
考查方向
解题思路
第一问由切线与直线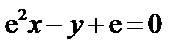
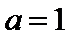
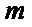
正确答案
略;
解析
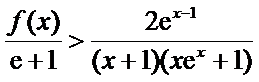
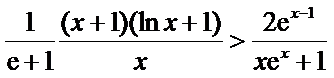
令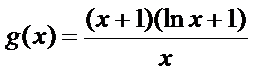
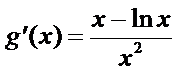
再令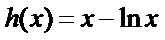
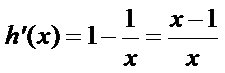
因为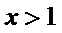
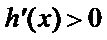
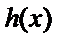
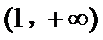
所以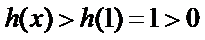
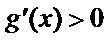
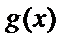
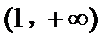
所以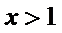
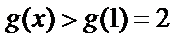

令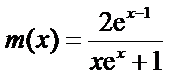

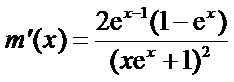
因为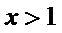
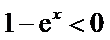
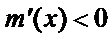
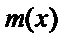
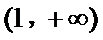
所以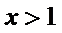
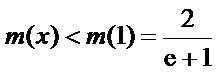
所以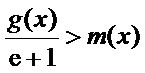
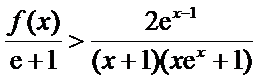
考查方向
解题思路
第二问现将不等式等级变形,构造新函数,对新函数用导函数求最值
12.已知函数





正确答案
解析


(1)当



(2)当













考查方向
解题思路
1.先求导后判断导数的正负,2.当导数有正有负时转化为一元二次方程根的分布处理,接着转化为线性规划使得问题得以解决。
易错点
1.不知道题中的条件:函数



知识点
已知函数
25.讨论
26.当





正确答案
(1)当






解析
(Ⅰ)函数


当



当





当


∴当






考查方向
解题思路
求导后根据a的范围讨论单调性即可;
易错点
问题中不讨论a的范围导致丢解;
正确答案
(2)
解析
(Ⅱ)当











则

由

记


记

∴



而




∴


而





考查方向
解题思路
先利用第(1)问的结论构造函数

易错点
不会构造函数
已知函数
27. 判断函数

28. 若

29.求证:
正确答案
(1)
解析
(Ⅰ)


考查方向
解题思路
直接求导后判断出
易错点
导后的函数不会变形为
正确答案
3;
解析
(Ⅱ)


令

又



当


∴

考查方向
解题思路
先分离参数后变为

易错点
无
正确答案
(3)略
解析
(Ⅲ)由(Ⅱ)知

令
∴
∴
考查方向
解题思路
根据第(2)问放缩
易错点
不会利用放缩法得到
设函数
26.若


27.当

28.若


正确答案
(1)
解析
(Ⅰ)若


得
考查方向
解题思路
根据导数的几何意义求解,
易错点
不清楚
正确答案
(2)


解析
(Ⅱ)由
当

当


由表可知:


所以,当


考查方向
解题思路
先求导,然后判断单调性后即可得到单调区间;
易错点
不清楚
正确答案
(3)略
解析
(Ⅲ)当

令
由指数函数及幂函数的性质知:

又




设


由
当


当


所以当
又
考查方向
解题思路
先将要求的函数变形为
易错点
不会构造函数解决问题,当所要的函数正负不确定时,不知道应该设零点解决。
扫码查看完整答案与解析


























