- 平面向量
- 共1314题
已知正数




正确答案
见解析
解析
证明:


知识点
如图是函数

正确答案
解析
由图知
将点
故选 C
知识点
在平面直角坐标系

正确答案
解析
由双曲线方程得

知识点
如图放置的正方形ABCD,AB =1.A,D分别在x轴、y轴的正半轴(含原点)上滑动,则
正确答案
2
解析
法一: 取



法二:设

知识点
在平面直角坐标系








(1)求曲线

(2)过定点









正确答案
(1)




解析
解析:(1)设


化简,得抛物线

令


令


所以,曲线



由题意可知,曲线
点


所以


(2)设







则

所以

设弦

因为



将②代入①,得

设

构造函数

由已知




当



知识点
已知椭圆


(1)若直线

(2)如果ΔBMN的重心恰好为椭圆的右焦点F,求直线
正确答案
(1)
解析
(1)由已知


∴


由

消去



∴所求弦长
(2)椭圆右焦点F的坐标为
设线段MN的中点为Q
由三角形重心的性质知

∴

求得Q的坐标为
设

且
以上两式相减得

故直线MN的方程为

知识点
已知




(1)求
(2)令


正确答案
见解析
解析
(1)设公差为d,公比为q,则
因为
所以
(2)
知识点
已知集合




正确答案
解析
由已知集合M是集合P的子集,设



知识点
已知向量


(1)求函数

(2)在












正确答案
见解析
解析





(2)





又

知识点
已知函数




(1)求
(2)若


(3)设




正确答案
(1)

解析
解析:(1)由题意:



只需sin
(2)由(1)得

由于
在


故

(3)构造函数

当


所以在


当m>0时,
因为


立,
故F(x)在


故m的取值范围是
另法:(3)
知识点
已知向量




正确答案
解析
略
知识点
在△ABC中,a,b,c是角A,B,C对应的边,向量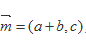
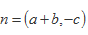
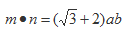
(1)求角C;
(2)函数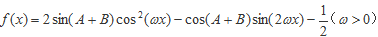
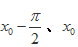
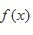
正确答案
见解析
解析
解析:(1)因为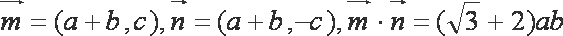
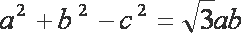
故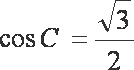
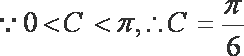
(2)
=
=
=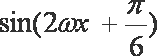
因为相邻两个极值的横坐标分别为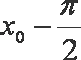
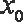
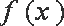
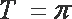
所以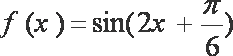
由
所以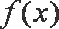
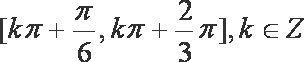
知识点
(本小题满分12分)
已知向量



(1)求函数f(x)的最小正周期;
(2)已知a,b,c分别为三角形ABC的内角对应的三边长,A为锐角,a=1,b=

正确答案
(1)
解析
(1)

因为

(2)由(1)知


由正弦函数图象可知,当



所以
由余弦定理


经检验均符合题意. ……………………10分
从而当



知识点
已知向量





正确答案
解析
解:设










知识点
已知向量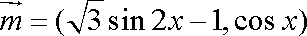
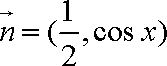
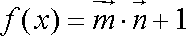
(1)求函数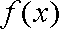
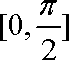
(2)已知在
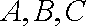
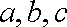
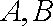
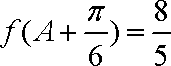
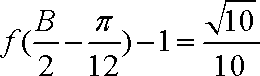
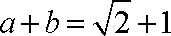
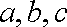
正确答案
见解析
解析
(1)函数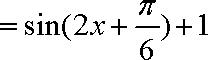
∴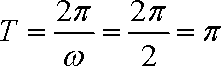
∵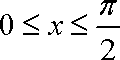
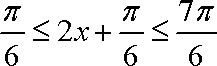
∴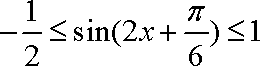
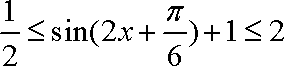
∴函数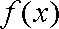
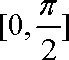
(2)∵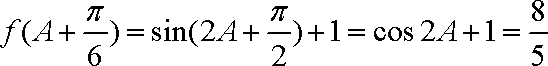
∴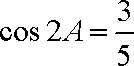
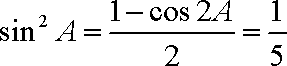
∵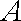
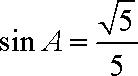
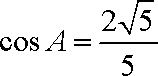
又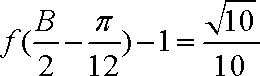
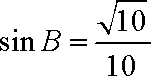
∵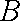
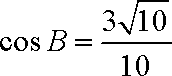
由正弦定理得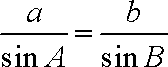
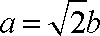
又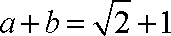
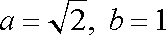
而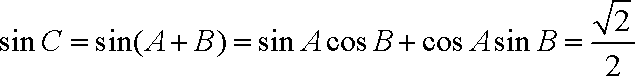
由正弦定理得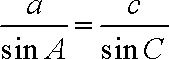
知识点
扫码查看完整答案与解析