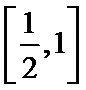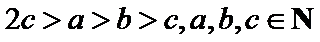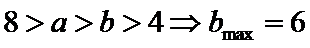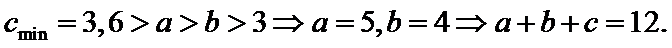- 真题试卷
- 模拟试卷
- 预测试卷
1.已知


正确答案
解析
因为

考查方向
解题思路
利用集合的补集运算即可求解.
易错点
注意端点的取值是否取到.
2.若复数

正确答案
解析
因为


考查方向
解题思路
利用复数四则运算和复数的几何意义即可求解.
易错点
易在计算时出现问题.
3.执行如图所示的程序框图,输出的
正确答案
解析
当




考查方向
解题思路
根据程序框图模拟程序即可求解.
易错点
易在模拟程序计算时出错.
7.设m, n为非零向量,则“存在负数
正确答案
解析
若







考查方向
解题思路
利用平面向量的夹角公式即可求解.
易错点
注意平面向量夹角公式的运用和取特殊角时的情况.
8.根据有关资料,围棋状态空间复杂度的上限M约为3361,而可观测宇宙中普通物质的原子总数N约为1080.则下列各数中与
(参考数据:lg3≈0.48)
正确答案
解析
设




考查方向
解题思路
利用对数的运算和对数的换底公式即可求解.
易错点
易在对数的运算和换底公式的运用上出现错误.
4.若


正确答案
解析
如图,画出可行域,




考查方向
解题思路
画出不等式组表示的可行域,根据目标函数的几何意义即可求解.
易错点
在求目标函数时易出现错误.
5.已知函数

正确答案
解析
因为


考查方向
解题思路
利用函数奇偶性和单调性即可求解.
易错点
注意函数的单调性和奇偶性的运用.
6.某三棱锥的三视图如图所示,则该三棱锥的体积为( )
正确答案
解析
该几何体是三棱锥,如图:
图中红色线围成的几何体为所求几何体,该几何体的体积是
考查方向
解题思路
利用几何体的三视图还原几何体,代入几何体的体积计算公式即可求解.
易错点
易在几何体图形的数据对应上出现错误.
9.在平面直角坐标系xOy中,角




正确答案
解析





考查方向
解题思路
根据角


易错点
易在两角之间的关系式和诱导公式的运用时出现问题.
10.若双曲线

正确答案
2
解析



考查方向
解题思路
根据双曲线的定义以及三个参数之间的关系即可求解.
易错点
易在计算时出现错误.
12.已知点P在圆

正确答案
6
解析

考查方向
解题思路
利用平面向量的数量积和三角函数的值域即可求解.
易错点
易在向量积的计算和夹角的取值出现问题.
13.能够说明“设a,b,c是任意实数.若a>b>c,则a+b>c”是假命题的一组整数a,b,c的值依次为
______________________________.
正确答案
-1,-2,-3(答案不唯一)
解析

考查方向
解题思路
取特殊值代入即可求解.
易错点
易在对题设的理解上出现错误.
11.已知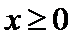
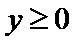
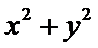
正确答案
解析
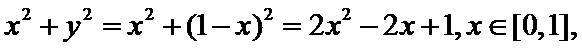
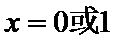
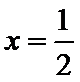
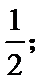
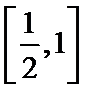
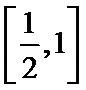
考查方向
解题思路
根据已知条件将式子进行化简,变形成关于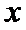
易错点
易在式子的变形和变量的取值范围出现错误.
14.某学习小组由学生和学科网&教师组成,人员构成同时满足以下三个条件:
(ⅰ)男学生人数多于女学生人数;
(ⅱ)女学生人数多于教师人数;
(ⅲ)教师人数的两倍多于男学生人数.
①若教师人数为4,则女学生人数的最大值为__________.
②该小组人数的最小值为__________.
正确答案
6,12
解析
设男生数,女生数,教师数为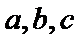
第一小问:
第二小问:
考查方向
解题思路
根据男生数,女生数,教师数之间的关系即可求解.
易错点
易在数值的取定上出现错误.
15.(本小题13分)
已知等差数列

(Ⅰ)求
(Ⅱ)求和:
正确答案
(1)

解析
(1)设公差为
(2)设




考查方向
(1)主要考查等差数列的性质和通项公式.
(2)主要考查等比数列的性质和求和公式.
解题思路
(1)设公差为
(2)设公比为



易错点
(1)易在代入通项公式的计算时出现错误.
(2)易在计算时出现错误.
17.(本小题13分)
某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),┄,[80,90],并整理得到如下频率分布直方图:
(Ⅰ)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(Ⅱ)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(Ⅲ)已知样本中有一半男生的分数学.科网不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例
正确答案
(1)0.4(2)20人(3)
解析
(1)根据频率分布直方图可知,样本中分数不小于70的频率为
所以从总体的400名学生中随机抽取一人,其分数小于70的概率估计为
(2)根据题意,样本中分数不小于50的频率为



(3)由题意可知,样本中分数不小于70的学生人数为
所以样本中分数不小于70的男生人数为
所以样本中的男生人数为


所以根据分层抽样原理,总体中男生和女生人数的比例估计为
考查方向
(1)主要考查频率分布直方图的性质.
(2)主要考查频率分布直方图的性质.
(3)主要考查分层抽样的性质.
解题思路
(1)根据频率分布直方图先求出频率,进一步求出求结果.
(2)利用频率计算出结果.
(3)利用频率分布直方图计算出每层人数,根据分层抽样的性质即可计算.
易错点
(1)易在频率的计算时出现错误(忘记乘以组距).
(2)以忽视低于40分的人数.
(3)易在每层的抽取时出现错误.
20.(本小题13分)
已知函数
(Ⅰ)求曲线

(Ⅱ)求函数

正确答案
(1)

解析
(1)因为



(2)设

当

所以

所以对任意


所以函数

因此



考查方向
(1)主要考查导数在某点出的几何意义.
(2)主要考查导数在函数单调性中的应用.
解题思路
(1)对函数求导,利用导数的几何意义即可求出切线方程.
(2)设

根据

易错点
(1)易在函数的求导和计算时出现错误.
(2)易在导函数的求取和符号判断时出现问题.
16.(本小题13分)
已知函数
(I)f(x)的最小正周期;
(II)求证:当

正确答案
(1) 
解析
(1)
所以

(2)因为
所以
所以
所以当

考查方向
(1)主要考查三角函数的周期
(2)主要考查三角函数的图象和性质.
解题思路
(1)利用两角和与差的正余弦公式化简即可求出函数的最小正周期.
(2)利用三角函数的图象性质进行求值即可.
易错点
易在函数的化简出现错误.易在三角函数的求值时出现错误.
18.(本小题14分)
如图,在三棱锥P–ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.
(Ⅰ)求证:PA⊥BD;(Ⅱ)求证:平面BDE⊥平面PAC;(Ⅲ)当PA∥平面BDE时,求三棱锥E–BCD的体积.
正确答案
(1)详见解析(2)详见解析(3)
解析
(1)证明:因为

(2)因为



由(I)知,


所以平面

(3)因为



所以
因为



由(I)知,



所以三棱锥

考查方向
(1)主要考查线面垂直的判定和性质.
(2)主要考查面面垂直的判定.
(3)主要考查棱锥的体积计算.
解题思路
(1)利用线面垂直的判定和性质即可得出结果.
(2)利用面面垂直的判定即可得出结果.
(3)利用线面平行的性质和锥体的体积计算公式即可得出结果.
易错点
(1)易在性质的应用时出错.
(2)易在条件的找取出现错误.
(3)易在锥体的体积计算时出错.
19.(本小题14分)
已知椭圆C的两个顶点分别为A(−2,0),B(2,0),焦点在x轴上,离心率为
(Ⅰ)求椭圆C的方程;(Ⅱ)点D为x轴上一点,过D作x轴的垂线交椭圆C于不同的两点M,N,过D作AM的垂线交BN于点E.求证:△BDE与△BDN的面积之比为4:5.
正确答案
(1)
解析
(1)设椭圆




(2)设

由题设知

直线



所以直线

直线

联立


由点


所以
又

所以


考查方向
(1)主要考查椭圆的标准方程.
(2)主要考查直线与椭圆的综合问题.
解题思路
(1)根据条件确定三个参数之间的关系,求出
(2)将直线方程与椭圆方程联立,利用韦达定理,结合三角形的面积公式,即可求出结果.
易错点
(1)根据条件确定三个参数时易出现错误.
(2)易在利用韦达定理计算时出现错误.