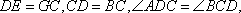- 平面与平面平行的判定与性质
- 共156题
1
题型:
单选题
|
已知四棱锥


正确答案
C
解析
可证四个面都是直角三角形,其面积
知识点
平面与平面平行的判定与性质
1
题型:
单选题
|
正确答案
D
解析
略
知识点
平面与平面平行的判定与性质
1
题型:简答题
|
正确答案
见解析
解析
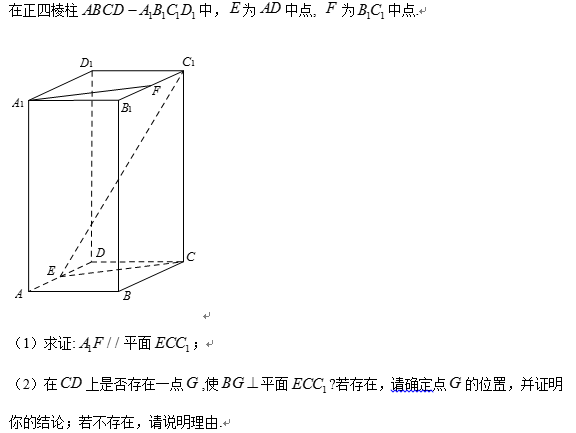
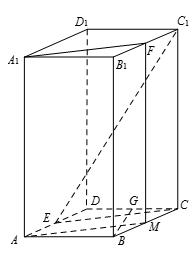
(1)证明:在正四棱柱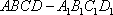
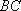
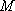
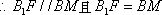

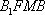
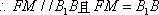
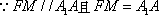

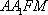
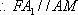
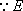
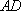
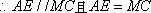

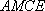
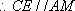
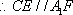
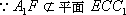
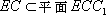
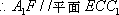
(2) 证明:在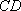
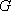
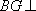
取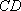
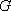
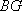
在正方形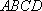
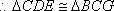
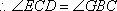
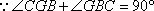
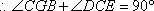
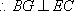
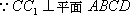
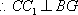
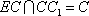
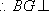
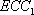
故在CD上存在中点G,使得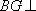
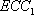
知识点
平面与平面平行的判定与性质
1
题型:简答题
|
已知四棱锥
(1)求此四棱锥的体积;
(2)若E是PD的中点,求证:
(3) 在(2)的条件下,若F是
正确答案
见解析。
解析
(1)由题意可知,四棱锥


(2)由三视图可知,

∵
又



∴

∵

又
又



∴

(3)∵


又∵


∴四边形



所以,直线AE和直线BF既不平行也不异面。
知识点
平面与平面平行的判定与性质
1
题型:简答题
|
已知向量 
(1)若

(2)若函数

正确答案
见解析。
解析
知识点
平面与平面平行的判定与性质
下一知识点 : 平行关系的综合应用
扫码查看完整答案与解析