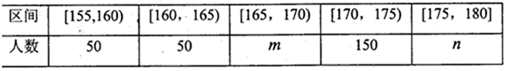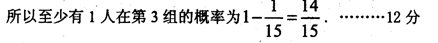- 判断两个函数是否为同一函数
- 共15题
已知函数
正确答案
解析
略
知识点
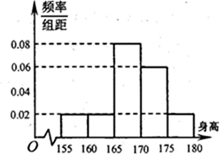
某学校组织500名学生体检,按身高(单位:cm)分组:第1组[155,160),第2组[160,165),第3组[165,170),第4组[170,175),第5组[175,180],得到的频率分布直方图如图所示。
(1)下表是身高的频数分布表,求正整数m,n的值;
(2)现在要从第1,2,3组中用分层抽样的方法抽取6人,第1,2,3组应抽取的人数分别是多少?
(3)在(2)的前提下,从这6人中随机抽取2人,求至少有1人在第3组的概率。
正确答案
见解析。
解析
知识点
已知函数
(1)求
(2)求函数
正确答案
(1)
(2)函数

解析
(1)由已知,得

(2)
函数

值域为
知识点
在股票市场上,投资者常参考股价(每一股的价格)的某条平滑均线(记作

























(1)请你帮老张算出

(2)
老张如能在今天以


正确答案
见解析。
解析
(1)




把


②

③








再由①,得 


于是,







(2)由(1)可知,

知识点
函数f(x)=cosx -log8x的零点个数为 。
正确答案
3
解析
略
知识点
设



正确答案
解析
略
知识点
如图,游客在景点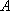
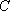
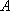
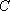
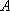
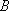
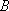
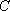
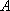
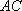
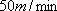

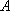
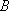
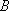
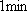
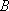
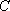
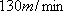
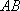
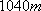
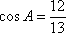
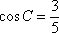
(1) 求山路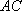
(2) 假设乙先到,为使乙在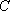

正确答案
见解析。
解析
(1) ∵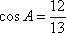
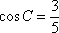
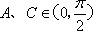
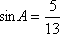
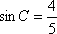
∴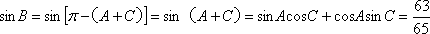
根据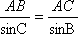
所以山路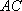
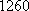
(2)由正弦定理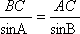
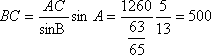
甲共用时间: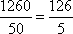
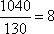
设乙的步行速度为 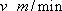
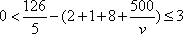
整理得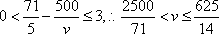
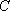
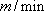
知识点
若函数


正确答案
解析
略
知识点
若点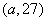
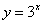
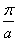
正确答案
解析
略
知识点
在



(1)求函数
(2)若
正确答案
(1)
(2)3
解析
(1)
因为

则所以当



(2)由题意知

又知


因为


由

知识点
扫码查看完整答案与解析