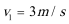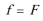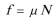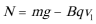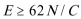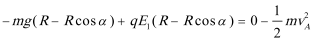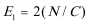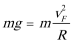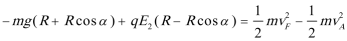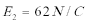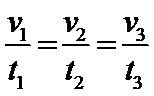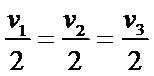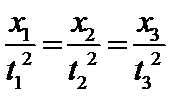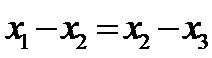- 匀变速直线运动的公式
- 共50题
今年春节前后,全国各地普降大雪,导致路面结冰,为避免事故要求汽车缓慢行驶。已知某汽车轮胎正常情况下与高速公路路面的动摩擦因数u1=0.8,在冰雪路面上动摩擦因数u2=0.2。该车司机发现前面有危险到开始制动需要0.5s(反应时间)。假设该车正以72km/h的速度匀速行驶。(假设刹车时车轮停止转动;g=10m/s2。)
13.如果该车在正常的路面上行驶,求司机从发现前面危险到停车的刹车距离。
14.如果该车在冰雪路面上行驶,某时刻司机发现前方40m有一辆车正以36km/h匀速行驶,司机开始刹车,是否会发生追尾事故。
正确答案
解析
①匀速阶段:
②减速阶段:

③总位移:
考查方向
匀变速直线运动规律的应用。
解题思路
汽车在反应时间内做匀速直线运动,刹车后做匀减速直线运动,结合匀速运动的位移和匀减速直线运动的位移之和求出司机从发现前面危险到停车的刹车距离.
易错点
关键抓住位移关系,结合运动学公式灵活求解.
正确答案
③△
解析
①以司机发现前车时刻为零时刻,则两车共速的时间t:


②t时间内两车各自位移:
③△
考查方向
匀变速直线运动规律的应用。
解题思路
根据牛顿第二定律求出刹车后的加速度大小,根据速度时间公式求出两车速度相等经历的时间,结合两车的位移关系判断是否发生追尾事故.
易错点
知道速度大者减速追及速度小者,若不相撞,速度相等时有最小距离.
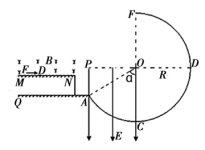
如图所示,水平地面QA与竖直面内的、半径R=4m的光滑圆轨道ACDF相连,FC为竖直直径,DO水平,AO与CO夹角α=600。QA上方有一水平台面MN,MN正上方分布着垂直纸面向里的匀强磁场,磁感强度B=4T。P是竖直线AP与DO的交点,PA的右侧、PO的下面、OC的左侧分布着竖直向下的、场强为E的匀强电场。一个质量m=2kg、电量q=+1C的小滑块(可视为质点)放在MN上,在水平推力F=4N的作用下正以速度V1向右作匀速运动。已知滑块与平台MN的滑动摩擦因数u=0.5;重力加速度g=10m/s2。
15.求小滑块在平台MN上的速度V1
16.小滑块从N点飞出后,恰从A点无碰撞地(沿轨道切线)进入圆轨道AC,为了使小滑块不向内脱离AF间的圆弧轨道,求电场强度E的取值范围
正确答案
解析
解: ①
②
③
由①②③解得:
考查方向
洛伦兹力,平衡条件。
解题思路
对小滑块受力分析,由平衡条件列式可求出。
易错点
解决本题的关键是小滑块以速度V1向右作匀速运动。
正确答案
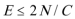
解析
①在A:
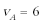
②小滑块不脱离AF的圆弧轨道,刚好滑到D点:VD=0m/s
解出:
③小滑块不脱离AF的圆弧轨道,刚好滑到F点:
解出:
④综上: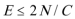
考查方向
磁场中的能量问题
解题思路
由动能定理和牛顿第二定理结合列方程计算。
易错点
小滑块从N到A做平抛运动,由平抛规律求A点的速度vA。
如图,一对表面粗糙的平行金属轨道竖直固定在水平地面上,轨道与地面绝缘,轨道顶端连接有一定值电阻R,在A1A2、A3A4区域内有垂直于轨道平面向里的匀强磁场.一水平金属杆CD通过两金属环套在轨道上,现使金属杆CD以某一初速度竖直向上运动,穿过磁场区域后继续上升到最高位置A5A6,然后落回地面,此后不再运动.已知金属杆CD与轨道间的摩擦力大小恒为其重力的
求:
29.金属杆CD向上、向下两次经过A3A4位置时的速度之比;
30.金属杆CD向上运动经过A1A2刚进入磁场时的加速度大小;
31.金属杆CD向上、向下两次经过磁场区域的过程中定值电阻R上产生的焦耳热之比.
正确答案
解析
(1)设杆的质量为m,A3A4与A5A6间的距离为h,上升过程中的加速度大小为:
又
则
下降过程中的加速度大小为:
又
则
即:
考查方向
电磁感应中的力学
解题思路
对金属杆受力分析,由牛顿第二定理求出加速度,然后由运动学公式计算出速度v,即可求出比值。
易错点
金属杆CD向上、向下两次经过A3A4位置时没有安培力。
正确答案
解析
设杆的长度为

回路中的电流
杆受到的安培力大小
杆向上经过A1A2刚进入磁场时,由牛顿第二定理得:
得
由题意知,杆下落进人磁场做匀速直线运动的速度v2,
切割产生的电动势为:
回路中的电流为:
杆受到的安培力:
这一过程杆受力平衡:
可得:
代入数据得:
考查方向
电磁感应中的力学
解题思路
对金属杆CD向上运动经过A1A2刚进入磁场时受力分析,结合欧姆定律和牛顿第二定理就可求出加速度a。
易错点
此题过程复杂,运动状态复杂,要仔细分析清楚各不同阶段的运动情况和受力情况。
正确答案
解析
设A3A2与A3A4的距离为d,杆向上穿过磁场的过程中,由动能定理

杆下落 过程中,
由功能关系得:
即
考查方向
电磁感应中的能量
解题思路
根据功能关系,定值电阻R上产生的焦耳热数值上等于安培力做的功。
易错点
不会应用常见的功能关系。
3.一质量为m的木块静止在光滑的水平面上,从t=0开始,将一个大小为F的水平恒力作用在该木块上,在t=t1时刻力F的瞬时功率是( )
正确答案
解析
由牛顿第二定律可以得到,F=ma,所以


考查方向
功率、平均功率和瞬时功率
解题思路
物体做匀加速直线运动,根据牛顿第二定律可以求得物体的加速度的大小,再由速度公式可以求得物体的速度的大小,由P=FV来求得瞬时功率.
易错点
计算平均功率和瞬时功率时一定要注意公式的选择,
知识点
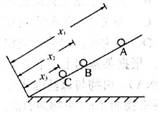
1.伽利略在研究自由落体运动时,做了如下实验。他让一个铜球从阻力很小(可忽略不计)的斜面上由静止开始滚下,并且重复做了上百次实验。假设某次实验中伽利略是这样做的:在斜面上任取三个位置A、B、C,如图所示。让小球分别由A、B、C位置从静止滚下,A、B、C与斜面底端的距离分别为xl、x2、x3。小球由A、B、C运动到斜面底端的时间分别为t1、t2、t3,速度分别为vl、v2、v3,则下列关系式中正确并且是伽利略用来证明小球沿光滑斜面向下运动是匀变速直线运动的是()
正确答案
解析
A、由v=at可得,
B、小球在斜面上三次运动的位移不同,末速度一定不同,故B错误;
C、由运动学公式可知,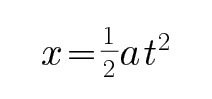
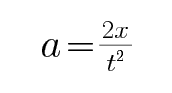
D、由图可知及运动学规律可知,x1-x2>x2-x3,故D错误;
考查方向
匀变速直线运动的位移与时间的关系
解题思路
小球在斜面上做匀变速直线运动,由运动学公式可判断各项是否正确;同时判断该结论是否由伽利略用来证明匀变速运动的结论.
易错点
掌握伽利略用来证明物体做匀变速直线运动的方法.
知识点
扫码查看完整答案与解析