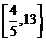- 求非线性目标函数的最值
- 共48题
4.若变量x，y满足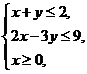
正确答案
知识点
12. 已知实数x，y满足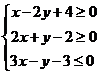
正确答案
知识点
12.已知实数
正确答案
解析
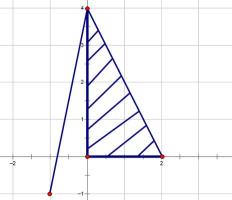
在平面直角坐标系中画出可行域如下
可以看出图中
图中
则
考查方向
解题思路
画出可行域，结合目标函数几何意义求最值。
易错点
注意最后要求距离的平方。
知识点
6.已知实数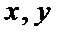
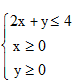
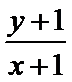
正确答案
解析
作出不等式组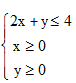
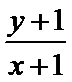
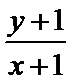
考查方向
解题思路
作出可行域，平行直线可得直线过点A（3，0）时，z取最大值，代值计算可得．
易错点
找不到什么时候取到最大值。
知识点
6．已知实数x、y满足约束条件
A[－
B[－1，
C（－∞，－1]∪[
D[－
正确答案
解析
如下图所示：
考查方向
解题思路
先画出可行域，再用数形结合法找到斜率的取值范围。
易错点
不会将目标函数转化为斜率来求解。
知识点
9.设实数x，y满足
A
B
C12
D14
正确答案
解析
画出可行域，在三角形ABC区域中结合图像可知
当动点在线段AC上时xy取得最大，此时2x＋y＝10，xy＝
当且仅当x＝
，故最大值为
考查方向
解题思路
先画出可行域，然后将目标函数用基本不等式转化后即可得到答案。
易错点
找不到xy与约束条件中的不等式之间的关系，导致没有思路。
知识点
15．若
正确答案
解析
由题意可知可行域如下图蓝色区域，所以可知
考查方向
解题思路
先作出不等式组所表示的平面区域，然后利用目标函数可取最值。
易错点
不等式的解法错误
知识点
13.若实数x，y满足
正确答案
1
解析
将
当直线
考查方向
解题思路
1)作出
2）由图象判定最优解与最优点；
3）再代入z=3x+2y.
易错点
本题易在求目标函数的最值时出现问题，注意目标函数的斜率与区域边界线的斜率比较
知识点
扫码查看完整答案与解析