- 焦耳定律
- 共3题
6.变压器能改变交变电流的电压和电流的大小。如图所示,有一台理想变
压器原、副线圈的匝数比为5:1,用理想电压表和理想电流表测量副线圈的电压和电流,R为副线圈的负载电阻。现在原线圈a、b两端加上交变电压μ,其随时间变化的规律为μ=220
正确答案
解析
A、由表达式知道周期

B、根据电压与匝数成正比可知,原线圈的电压的最大值为

C、电流与匝数成反比,所以若电流表示数为0.1A,则原线圈中的电流为0.02A,故C错误;
D、副线圈消耗的电能全部转化为焦耳热,所以Q=UIt=44×0.1×60=264J,故D正确.
考查方向
变压器的构造和原理;电功、电功率;焦耳定律
解题思路
根据图象可以求得输出电压的有效值、周期和频率等,再根据电压与匝数成正比,电流与匝数成反比,即可求得结论.
易错点
本题关键掌握理想变压器的电压、电流与匝数之间的关系,正弦式交流电最大值和有效值之间的关系.
知识点
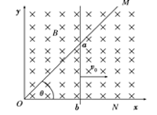
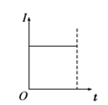
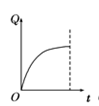
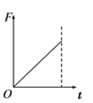
7. 如图所示,顶角θ=45°的金属导轨MON固定在水平面内,导轨处在方向竖直向下、磁感应强度为B的匀强磁场中.一根与ON垂直的导体棒在水平外力作用下以恒定速度v0沿导轨MON向右滑动,导体棒的质量为m,导轨与导体棒单位长度的电阻均为r.导体棒与导轨接触点为a和b,导体棒在滑动过程中始终保持与导轨良好接触.t=0时导体棒位于顶角O处,则流过导体棒的电流强度I、导体棒内产生的焦耳热Q、导体棒做匀速直线运动时水平外力F、导体棒的电功率P各量大小随时间变化的关系正确的是
正确答案
解析
A、0到t时间内,导体棒的位移为:x=v0t
t时刻,导体棒的长度为:l=x
导体棒的电动势为:E=Blv0
回路总电阻为:R=(2x+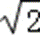
电流强度为: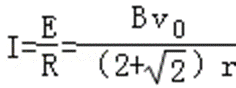
C、导体棒匀速直线运动,水平外力与安培力二平衡,则有: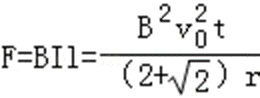
D、t时刻导体棒的电功率:P=I2R′=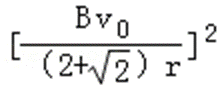
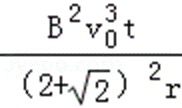
B、因为:P∝t
所以:Q=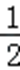
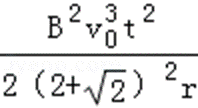
考查方向
解题思路
求出t时刻导体棒的有效长度,结合切割产生的感应电动势和闭合电路欧姆定律求出电流强度与时间的关系式.
导体棒在0~t时间内电流大小恒定,抓住R与时间正比,通过平均功率,根据Q=Pt求出产生的焦耳热Q.
导体棒做匀速直线运动时,水平外力等于安培力,根据平衡条件求出水平拉力的表达式
易错点
综合考查了切割产生的感应电动势、闭合电路欧姆定律、牛顿第二定律等知识点,综合性较强,关键得到感应电流不变
知识点
如图所示,竖直平面内有足够长、不计电阻的两组平行光滑金属导轨,宽度均为L=0.5m,上方连接一个阻值R=1Ω的定值电阻,虚线下方的区域内存在垂直纸面向里的磁感应强度B=2T的匀强磁场。完全相同的两根金属杆1和2靠在导轨上,金属杆长与导轨等宽且与导轨接触良好,电阻均为r =0.5Ω。将金属杆1固定在磁场的上边缘(仍在此磁场内),金属杆2从磁场边界上方h0=0.8m处由静止释放,进入磁场后恰作匀速运动。(g取10m/s2)求:
(1)金属杆的质量m;
(2)若金属杆2从磁场边界上方h1=0.2m处由静止释放,进入磁场下落一段距离后做匀速运动。在金属杆2加速的过程中整个回路产生了1.4J的电热。求此过程中流过电阻R的电荷量q;
(3)若金属杆2仍然从磁场边界上方h1=0.2m处由静止释放,在金属杆2进入磁场的同时释放金属杆1,试求两根金属杆各自的最大速度。
正确答案
见解析。
解析
(1)金属杆2进入磁场前做自由落体运动,进入磁场的速度
vm=

金属杆2进入磁场后切割磁感线,回路中产生感应电流,有
感应电动势E=BLvm,感应电流
金属杆恰做匀速运动,受安培力和重力平衡:mg=BIL
解出m=

(2)金属杆2自由下落h1,进入磁场,做加速运动,设金属杆2在磁场内下降h2后达到匀速运动,在加速的过程中,部分机械能转化为电能产生电热,有
mg(h1+h2)=
可得 h2=
金属杆2进入磁场到匀速运动的过程中

解出流过电阻的电量 q=

(3)金属杆2刚进入磁场时的速度v=

金属杆2进入磁场同时释放金属杆1后,回路中有感应电流,两杆都受安培力和重力,且受力情况相同,都向下做加速运动,随速度增大,感应电流增大,安培力增大,直到安培力和重力相等时,速度达到最大。
金属杆1和2产生的感应电动势为E1=BLv1,E2=BLv2
感应电流为
达到最大速度时杆的重力等于安培力
mg=BIL
整理得到:v1+ v2=
代入数据得v1+ v2=4 m/s……………… ①
因为两个金属杆任何时刻受力情况相同,因此任何时刻两者的加速度也都相同,在相同时间内速度的增量也必相同,即:v1-0 =v2- v
代入数据得v2= v1+2……………………………………………………… ②
① ②两式联立求出:v1=1m/s,v2=3m/s
知识点
扫码查看完整答案与解析