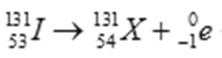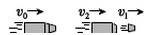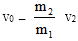- 动量守恒定律
- 共299题
(1)碘131核不稳定,会发生β衰变,其半衰变期为8天。
①碘131核的衰变方程: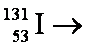
②经过_______天有75%的碘131核发生了衰变。
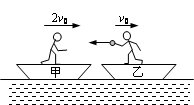
(2)如图所示,甲、乙两船的总质量(包括船、人和货物)分别为10m、12m,两船沿同一直线同一方向运动,速度分别为2v0、v0。为避免两船相撞,乙船上的人将一质量为m的货物沿水平方向抛向甲船,甲船上的人将货物接住,求抛出货物的最小速度
正确答案
(1)①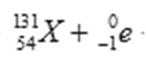
(2)4v0
解析
(1)①核衰变遵守电荷量和质量数守恒,所以
② 根据半衰期概念,得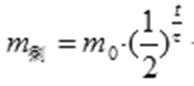

(2)解析:设乙船上的人抛出货物的最小速度为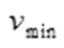
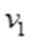
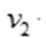
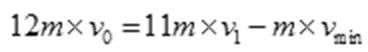
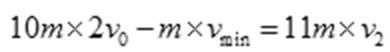
为避免两船相撞应满足: 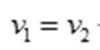
联立①②③式得: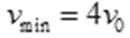
知识点
冰球运动员甲的质量为80.0kg。当他以5.0m/s的速度向前运动时,与另一质畺为100kg、速度为3.0m/s的迎面而来的运动员乙相撞。碰后甲恰好静止。假设碰撞时间极短,求:
(1)碰后乙的速度的大小;
(2)碰撞中总机械能的损失。
正确答案
(1)设运动员甲、乙的质量分别为m、M,碰前速度大小分别为v、V,碰后的速度大小为

代入数据得 
(2)设碰撞过程中总机械能的损失为

联立①②③式,代入数据得

(评分标准:①②③④式各3分。)
解析
略。
知识点
(1)关于原子核的结合能,下列说法正确的是
a.原子核的结合能等于使其完全分解成自由核子所需的最小能量
b.一重原子核衰变成α粒子和另一原子核,衰变产物的结合能之和一定大于原来重核的结合能
c. 铯原子核(

d.比结合能越大,原子核越不稳定
e.自由核子组成原子核时,其质量亏损所对应的能量大于该原子核的结合能
(2)如图,光滑水平直轨道上有三个质量均为m的物块A、B、C。 B的左侧固定一轻弹簧(弹簧左侧的挡板质最不计)。设A以速度V0朝B运动,压缩弹簧;当A、 B速度相等时,B与C恰好相碰并粘接在一起,然后继续运动。假设B和C碰撞过程时间极短。求从A开始压缩弹簧直至与弹簧分离的过程中,
① 整个系统损失的机械能;
② 弹簧被压缩到最短时的弹性势能。
正确答案
答案:(1)ABC
(2)
(3)
解析
略
知识点
如图所示,空间有场强













(1)求碰撞前瞬间小球
(2)若小球

(3)若施加恒力后,保持平板垂直于纸面且与水平面的夹角不变,在

正确答案
见解析
解析
(1)
设P的加速度为a0、到D点的竖直速度为vy,合速度大小为v1,与水平方向的夹角为β,有
联立上述方程,代入数据解得:v1=6m/s
β=300
(2)设A碰前速度为v2,此时轻绳与竖直线的夹角为β,由动能定理得:
设A、P碰撞后小球C的速度为v,由动量守恒定律得:
小球C到达平板时速度为0,应做匀减速直线运动,设加速度的大小为a 有

设恒力大小为,F与竖直方向的夹角为α,如图,根据牛顿第二定律,得:
代入相关数据解得:
(3)由于平板可距D点无限远,小球C必做匀速或匀加速直线运动,恒力F1的方向可从竖直方向顺时针转向无限接近速度方向,设恒力与速度方向夹角为θ,有:
在垂直于速度方向上,有:
则F1的大小满足条件为


知识点
如图所示,装置的左边是足够长的光滑水平面,一轻质弹簧左端固定,右端连接着质量 M=2kg的小物块A。装置的中间是水平传送带,它与左右两边的台面等高,并能平滑对接。传送带始终以n=2m/s 的速度逆时针转动。装置的右边是一光滑的曲面,质量m=1kg的小物块B从其上距水平台面h=1.0m处由静止释放。已知物块B与传送带之间的摩擦因数 n=0.2, f=1.0m。设物块A、B中间发生的是对心弹性碰撞,第一次碰撞前物块A静止且处于平衡状态。取g=10m/s2。
(1)求物块B与物块A第
(2)一次碰撞前的速度大小;通过计算说明物块B与物块A第一次碰撞后能否运动到右边曲面上?
(3)如果物块A、B每次碰撞后,物块A再回到平衡位置时都会立即被锁定,而当他们再次碰撞前锁定被解除,试求出物块B第n次碰撞后运动的速度大小。
正确答案
(1)4 m/s
(2)不能
(3)
解析
(1)设物块B沿光滑曲面下滑到水平位置时的速度大小为v0,由机械能守恒知mgh=

设物块B在传送带上滑动过程中因受摩擦力所产生的加速度大小为a
μmg=ma③
设物块B通过传送带后运动速度大小为v,有
v2-v02=-2al④
结合②③④式解得v=4 m/s⑤
由于v>u=2 m/s,所以v=4 m/s即为物块B与物块A第一次碰撞前的速度大小。
(2)设物块A、B第一次碰撞后的速度分别为V、v1,取向右为正方向,由弹性碰撞知
-mv=mv1+MV⑥

解得
即碰撞后物块B沿水平台面向右匀速运动。
设物块B在传送带上向右运动的最大位移为l′,则
0-v12=-2al′⑨

所以物块B不能通过传送带运动到右边的曲面上。
(3)当物块B在传送带上向右运动的速度为零后,将会沿传送带向左加速,可以判断,物块B运动到左边台面时的速度大小为v1,继而与物块A发生第二次碰撞,设第二次碰撞后物块B速度大小为v2,同上计算可知
物块B与物块A第三次碰撞、第四次碰撞…,碰撞后物块B的速度大小依次为

则第n次碰撞后物块B的速度大小为

知识点
如图所示,质量M=2kg的滑块套在光滑的水平轨道上,质量m=1kg的小球通过长L=0.5m的轻质细杆与滑块上的光滑轴O连接,小球和轻杆可在竖直平面内绕O轴自由转动。开始轻杆处于水平状态。现给小球一个竖直向上的初速度v0=4m/s,g取10m/s2。
(1)若锁定滑块,试求小球通过最高点P时对轻杆的作用力大小和方向。
(2)若解除对滑块的锁定,试求小球通过最高点时的速度大小。
(3)在满足(2)的条件下,试求小球击中滑块右侧轨道位置点与小球起始位置点间的距离。
正确答案
见解析。
解析
(1)设小球能通过最高点,且此时的速度为v1。在上升过程中,因只有重力做功,小球的机械能守恒。则
设小球到达最高点时,轻杆对小球的作用力为F,方向向下,则F+mg=
联立解得F=2N,由牛顿第三定律可知,小球对轻杆的作用力大小为2N,方向竖直向上。
(2)解除锁定后,设小球通过最高点时的速度为v2,此时滑块的速度为V。在上升过程中,因系统在水平方向上不受外力作用,水平方向的动量守恒。以水平向右的方向为正方向,有
mv2+MV=0
在上升过程中,因只有重力做功,系统的机械能守恒,则

(3)设小球击中滑块右侧轨道的位置点与小球起始点的距离为s1,滑块向左移动的距离为s2,任意时刻小球的水平速度大小为v3,滑块的速度大小为V/。由系统水平方向的动量守恒,得
mv3-MV′=0,两边同乘以△t,得mv3△t-MV′△t=0,故对任意时刻附近的微小间隔△t都成立,累积相加后,有ms1-Ms2=0,又s1+s2=2L,得s1=
知识点
光滑水平面上两小球a、b用不可伸长的松弛细绳相连。开始时a球静止,b球以一定速度运动直至绳被拉紧,然后两球一起运动,在此过程中两球的总动量________(填“守恒”或“不守恒”);机械能________(填“守恒”或“不守恒”)。
正确答案
守恒;不守恒
解析
将a b组成系统,对系统受力分析知合外力为零,故系统动量守恒;而在此过程拉力对b做负功,机械能不守恒。
知识点
质量为M的物块静止在光滑水平桌面上,质量为m的子弹以水平速度v0射入物块后,以水平速度2v0/3射出。则物块的速度为____,此过程中损失的机械能为____。
正确答案

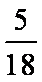
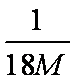
解析
由动量守恒定律,m v0=m·2v0/3+Mv,解得v=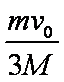
由能量守恒定律,此过程中损失的机械能为△E= 
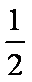
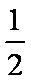
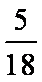
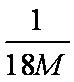
知识点
(1)恒星向外辐射的能量来自于其内部发生的各种热核反应,当温度达到108K时,可以发生“氦燃烧”。
①完成“氦燃烧”的核反应方程:
②


(2)如图所示,光滑水平轨道上放置长木板A(上表面粗糙)和滑块C,滑块B置于A的左端,三者质量分别为



正确答案
见解析。
解析
(1)


(2)因碰撞时间极短,A与C碰撞过程动量守恒,设碰后瞬间A的速度为vA,C的速度为vC,以向右为正方向,由动量守恒定律得

A与B在摩擦力作用下达到共同速度,设共同速度为vAB,由动量守恒定律得

A与B达到共同速度后恰好不再与C碰撞,应满足

联立上式,代入数据得

知识点
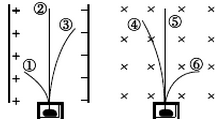
(1)如图,放射性元素镭衰变过程中释放出α、β、γ三种射线,分别进入匀强电场和匀强磁场中,下列说法正确的是_______。(填选项前的字母)
A. ①表示γ射线,③表示α射线
B. ②表示β射线,③表示α射线
C. ④表示α射线,⑤表示γ射线
D. ⑤表示β射线,⑥表示α射线
(2)一枚火箭搭载着卫星以速率v0进入太空预定位置,由控制系统使箭体与卫星分离。已知前部分的卫星质量为m1,后部分的箭体质量为m2,学科网分离后箭体以速率v2沿火箭原方向飞行,若忽略空气阻力及分离前后系统质量的变化,则分离后卫星的速率v1为_______。(填选项前的字母)
A. V0-V2
B. V0+V2
C.
D.
正确答案
解析
(1)α射线带正电,β射线带负电,γ射线不带电。在匀强电场中,α射线与β射线分别在电场力的作用下发生偏转,α射线偏向负极板,β射线偏向正极板,γ射线不受电场力,不发生偏转;在磁场中,由左手定则可以判断α射线向左偏,β射线向右偏,γ射线不受洛伦兹力,不发生偏转。故C项正确。
(2)忽略空气阻力和分离前后系统质量的变化,卫星和箭体整体分离前后动量守恒,则有(m1+m2)v0=m1v1+m2v2,整理可得v1=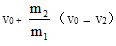
知识点
扫码查看完整答案与解析