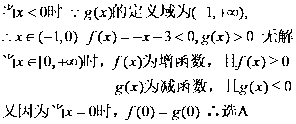- 对数函数的图像与性质
- 共30题
5．函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4.当a>1时，函数y=ax与函数y=logax的图象的交点个数（ ）
正确答案
解析
假定y=ax与y=x相切于(x0，y0)，则切线方程为y-
①当
②当
③当1<a<
于是，正确的答案为A.
知识点
3.当0<x≤
A(0，
B(
C(1，
D(
正确答案
解析
∵0<x≤
∴0<a<1，排除答案C，D；
取a=
显然4x<logax不成立，排除答案A；
故选B.
知识点
15.若不等式logax>sin2x(a>0，a≠1)对任意x∈(0，
正确答案
解析
记y1=logax，y2=sin2x，原不等式相当于y1>y2
作出两个函数的图象，如图所示
可知当y1=logax过点A(
所以当
知识点
5.函数f(x)= 
正确答案
解析
当x≤0时，令x2+3x+2=0⇒x=- 1或x=- 2;
当x>0时，令4－x+ln x=0⇒ln x=x－4
通过图象可知有两个交点，此时也有两个根.
所以已知函数有4个零点.
知识点
9.已知函数y=f(x)的周期为2，当x∈[-1，1]时，f(x)=x2，那么函数y=f(x)的图象与函数y=|lg x|的图象的交点共有 个。
正确答案
10
解析
在同一坐标系中作出函数y=f(x)，y=|lg x|的图象如图，由图象可知，两个函数的图象的交点共有10个.
知识点
9.若函数f(x)=|2x-1|，则函数g(x)=f(f(x))+lnx在(0，1)上不同的零点个数为 。
正确答案
3
解析
将函数g(x)=f(f(x))+lnx在(0，1)上不同的零点个数转化为函数y=f[f(x)]的图象在(0，1)上与y=-lnx的图象的交点个数，作出图象如图
可知两个函数图象在(0，1)上有3个交点，即不同的零点个数为3.
知识点
11.设
则下列关系式中正确的是（ ）
A
B
C
D
正确答案
解析
然后再比较
利用均值不等式得到
自然对数底数大于1，所以单调递增，所以
考查方向
解题思路
易错点
对数的基本运算不会，判断不出
知识点
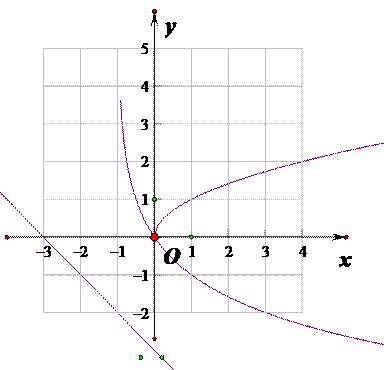
6.函数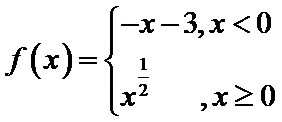
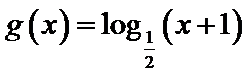
正确答案
解析
根据题意可知
考查方向
解题思路
【解题思路】本题函数的单调性及其性质解题，
画出函数图像不难分析得出答案，如图：
易错点
该题出错在分段不清，对数函数不熟悉
知识点
9．已知
A
B
C
D
正确答案
解析
因为
考查方向
本题主要考查了函数的单调性和比较大小。
易错点
本题易在判定
知识点
扫码查看完整答案与解析