- 古典概型的概率
- 共218题
根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险但不购买甲种保险的概率为0.3.设各车主购买保险相互独立。
(1)求该地1位车主至少购买甲、乙两种保险中的1种的概率;
(2)求该地3位车主中恰有1位车主甲、乙两种保险都不购买的概率。
正确答案
(1) 0.8;(2)0.384
解析
记A表示事件:该地的1位车主购买甲种保险:
B表示事件:该地的1位车主购买乙种保险但不购买甲种保险。
C表示事件:该地的1位车主至少购买甲、乙两种保险中的1种;
D表示事件:该地的1位车主甲、乙两种保险都不购买;
E表示事件:该地的3位车主中恰有1位车主甲、乙两种保险都不购买。
(1)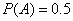
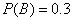
(2)D=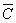
P(E)=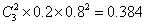
知识点
下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天。
(1)求此人到达当日空气质量优良的概率;
(2)求此人在该市停留时间只有1天空气重度污染的概率;
(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结果不要求证明)
正确答案
见解析
解析
(1)在3月1日至3月13日这13天中,1日、2日、3日、7日、12日、13日共6天的空气质量优良,所以此人到达当日空气质量优良的概率是
(2)根据题意,事件“此人在该市停留期间只有1天空气重度污染”等价于“此人到达该市的日期是4日,或5日,或7日,或8日”。
所以此人在该市停留期间只有1天空气重度污染的概率为
(3)从3月5日开始连续三天的空气质量指数方差最大。
知识点
设



(1)求概率
(2)求

正确答案
(1)
解析
(1)若两条棱相交,则交点必为正方体8个顶点中的一个,过任意1个顶点恰有3条棱,
∴共有
∴ 
(2)若两条棱平行,则它们的距离为1或

∴ 

∴随机变量
∴其数学期望
知识点
从1,2,3,4,5中任意取出两个不同的数,其和为5的概率是__________。
正确答案
0.2
解析
该事件基本事件空间Ω={(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)}共有10个,记A=“其和为5”={(1,4),(2,3)}有2个,∴P(A)=
知识点
在3张奖券中有一、二等奖各1张,另1张无奖,甲、乙两人各抽取1张,两人都中奖的概率是______________;
正确答案
解析
基本事件的总数是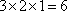
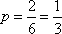
知识点
扫码查看完整答案与解析