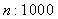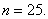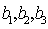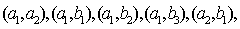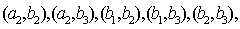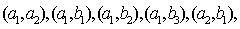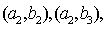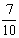- 古典概型的概率
- 共218题
某网站就观众对2011年春晚小品类节目的喜爱程度进行网上调查,其中持各种态度的人数如下表:
(1)现用分层抽样的方法从所有参与网上调查的观众中抽取了一个容量为n的样本,已知从不喜欢小品的观众中抽取的人数为5人,则n的值为多少?
(2)在(1)的条件下,若抽取到的5名不喜欢小品的观众中有2名为女性,现将抽取到的5名不喜欢小品的观众看成一个总体 ,从中任选两名观众,求至少有一名为女性观众的概率.
正确答案
见解析。
解析
(1)采用分层抽样的方法,样本容量与总体容量的比为
则不喜爱小品观众应抽取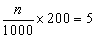
∴
(2)由题意得,女性观众抽取2人,男性观众抽取3人,
设女性观众为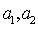
则从5位不喜爱小品的观众中抽取两名观众有10种可能:
其中抽取两名观众中至少有一名为女性观众有7种可能:
所以从5位不喜爱小品的观众中抽取两名观众,
至少有一名为女性观众的概率为
知识点
高三某班有学生56人,现将所有同学随机编号,用系统抽样的方法,抽取一个容量为4的样本,已知5号、33号、47号学生在样本中,则样本中还有一个学生的编号为
正确答案
解析
略
知识点
在某次测量中得到的
若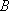
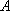
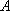
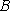
正确答案
解析
由方差意义可知,选D.
知识点
参加市数学调研抽测的某校高三学生成绩分析的茎叶图和频率分布直方图均受到不同程度的破坏,但可见部分信息如下,据此解答如下问题:
(1)求参加数学抽测的人数


(2)若从分数在

正确答案
见解析。
解析
(1)分数在


由

茎叶图可知抽测成绩的中位数为



参加数学竞赛人数




(2)设“在


将




在


其中,恰好有一人分数在

故所求的概率得
答:恰好有一人分数在

知识点
甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为l50,边界忽略不计)即为中奖。
乙商场:从装有3个白球3个红球的盒子中一次性摸出2球(球除颜色外不加区分),如果摸到的是2个红球,即为中奖。
问:购买该商品的顾客在哪家商场中奖的可能性大?
正确答案
见解析。
解析
知识点
扫码查看完整答案与解析