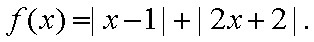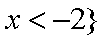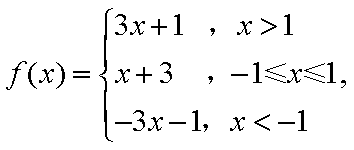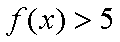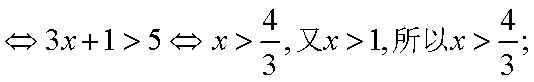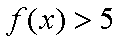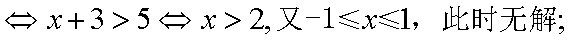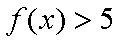- 分式不等式的解法
- 共109题
1
题型:简答题
|
已知函数
(1)解不等式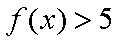
(2)若不等式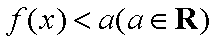
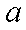
正确答案
(1)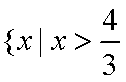
(2)(-∞,2]
解析
(1)根据条件
当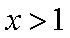
当
当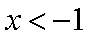
综上,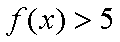
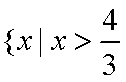
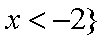
(2)由于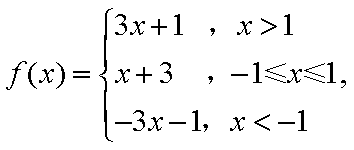
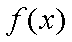
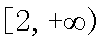
又不等式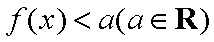

知识点
分式不等式的解法
1
题型:填空题
|
已知实数x,y满足
正确答案
1
解析
略
知识点
分式不等式的解法
1
题型:简答题
|
在直角坐标系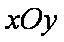
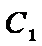
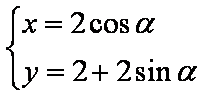
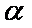
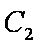
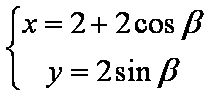
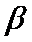
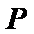
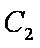

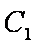
(1)求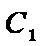
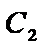
(2)在以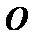
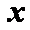
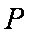
正确答案
见解析。
解析
(1)曲线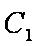
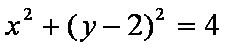
曲线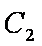
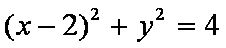
两圆的公共弦所在直线为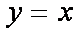
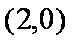
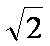
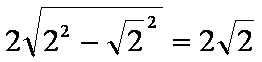
(2)曲线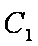
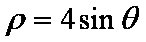
曲线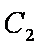
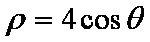
设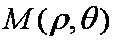
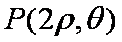
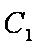
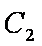
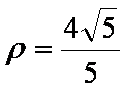
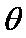
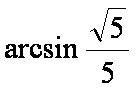
所以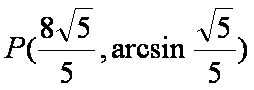
知识点
分式不等式的解法
1
题型:简答题
|
已知函数
(1)若不等式


(2)在(1)的条件下,若存在实数


正确答案
(1)a=1(2)[4,+∞)
解析
(1)由条件知

(2)由(1)得


若存在实数


而

因此实数

知识点
分式不等式的解法
1
题型:填空题
|
一般地,如果函数



①

③

⑤
正确答案
②③⑤
解析
对于①,其值域为

故②正确;对于③,



单调递减,在




不符合题意,故④舍去;对于⑤,

(当且仅当

知识点
分式不等式的解法
下一知识点 : 一元高次不等式的解法
扫码查看完整答案与解析