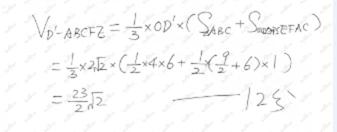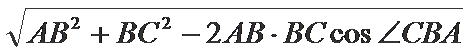- 直线与平面垂直的判定与性质
- 共118题
17.
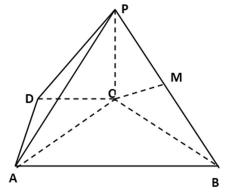
如图,在四棱锥P-ABCD中,PA⊥CD,AD∥BC,∠ADC=∠PAB=90°,BC=CD=½AD。
(I)在平面PAD内找一点M,使得直线CM∥平面PAB,并说明理由;
(II)证明:平面PAB⊥平面PBD。
正确答案
知识点
16.如图,在正方体ABCD−A1B1C1D1中,E、F分别为BC、BB1的中点,
则下列直线中与直线EF相交的是( )
正确答案
解析
直线B1C1和直线EF在同一平面内,又不平行,所以一定相交,其余选项都是异面直线.
考查方向
解题思路
空间直线的位置关系
易错点
空间想象
知识点
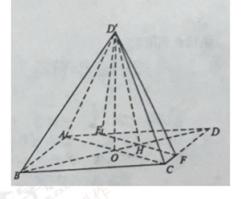
19. 如图,菱形ABCD的对角线AC与BD交于点O,点E,F分别在AD,CD上,AE=CF,EF交BD于点H,将△DEF沿EF折到△D′EF的位置.
(I)证明: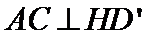
(II)若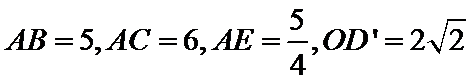
正确答案
知识点
18. 在如图所示的几何体中,D是AC的中点,EF∥DB.
(I)已知AB=BC,AE=EC.求证:AC⊥FB;
(II)已知G,H分别是EC和FB的中点.求证:GH∥平面ABC.
正确答案
(Ⅰ))证明:见解析;(Ⅱ)见解析.
解析
试题分析:(Ⅰ))根据








(Ⅱ)设








试题解析:(Ⅰ))证明:因













(Ⅱ)设



















考查方向
知识点
16.在四棱锥P-ABCD中,PC⊥平面ABCD,DC∥AB,DC=2,AB=4,BC=2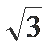
(1)求证:AC⊥PB;
(2)若PC=2,点M是棱PB上的点,且CM∥平面PAD,求BM的长。
正确答案
见解析
解析
(1)∵PC⊥平面ABCD,∴PC⊥AC,
又∠CBA=30°,BC=2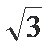
∴AC=
=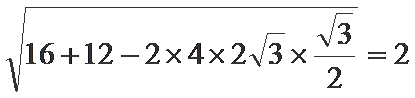
∴AC2+BC2=4+12=16=AB2,∴∠ACB=90°,
故AC⊥BC.又∵PC、BC是平面PBC内的两条相交直线,
故AC⊥平面PBC,∴AC⊥PB.
(2) BM=2
考查方向
解题思路
(1)由余弦定理求AC
(2)由勾股逆定理得∠ACB=90°
(3)AC⊥BC,PC⊥AC,AC⊥平面PBC,∴AC⊥PB
易错点
证明过程不到位。
知识点
扫码查看完整答案与解析