- 曲线的方程
- 共349题
曲线

正确答案
(3,

解析
解:联立两函数的解析式,可得:
解得
即曲线



故答案为:(3,

已知曲线C的方程为:x2+y2-2|x|-2|y|=0,P1、P2是曲线C上的两个点,则|P1P2|的最大值为______.
正确答案
解析
解:利用绝对值的几何意义可知曲线C表示x2+y2-2x-2y=0,x2+y2+2x|-2y=0,x2+y2+2x+2y=0,x2+y2-2x+2y=0,分别在各个象限的部分(包括与坐标轴的交点)
∵P1、P2是曲线C上的两个点,
∴|P1P2|的最大值为一、三(或二、四)象限的圆的圆心距加上2个半径的长
∴|P1P2|的最大值为2



故答案为:
平面上动点A(x,y)满足

正确答案
解析



∵B(-4,0),C(4,0),
∴|AB|+|AC|≤10,当且仅当A为(0,±3)时,等号成立.
故选:B.
设A、B分别是直线y=




正确答案
解:设P(x,y),因为A,B分别是直线y=

故可设
又

因为
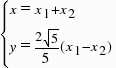

代入①得:

解析
解:设P(x,y),因为A,B分别是直线y=

故可设
又

因为
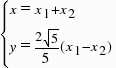

代入①得:

方程
正确答案
解析
解:由
得
即
也就是动点(x,y)到定点(-3,1)的距离与到定直线x-y+3=0的距离的比等于
符合双曲线的定义,
∴该方程表示的曲线是双曲线.
故选:C.
扫码查看完整答案与解析



