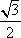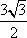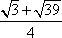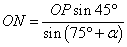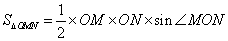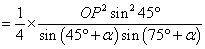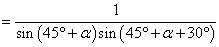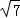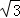- 解三角形
- 共459题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
在△ABC中,角A,B,C的对边分别为a,b,c,角A,B,C成等差数列。
(1)求cosB的值;
(2)边a,b,c成等比数列,求sinAsinC的值。
正确答案
(1) 
解析
(1)由已知2B=A+C,A+B+C=180°,解得B=60°,
所以
(2)解法一:由已知b2=ac,及
根据正弦定理得sin2B=sinAsinC,
所以sinAsinC=1-cos2B=
解法二:由已知b2=ac,及
根据余弦定理得
所以A=C=B=60°,故sinAsinC=
知识点
如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练,已知点A到墙面的距离为AB,某目标点










正确答案
解析
由勾股定理知,





则



所以


故

知识点
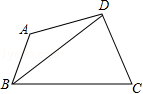
在△ABC中,AC=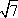
正确答案
解析
设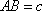
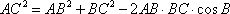
即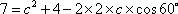
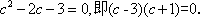
设BC边上的高等于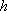
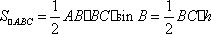
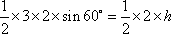
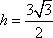
知识点
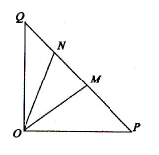
如图,在等腰直角三角形
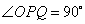
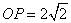
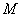

(1)若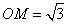

(2)若点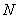
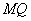
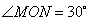

正确答案
见解析
解析
本小题主要考查解三角形、同角三角函数的基本关系、两角和与差的三角函数等基础知识,考查推理论证能力、抽象概括能力、运算求解能力,考查函数与方程思想、数形结合思想、化归与转化思想,满分12分。
(1)在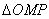
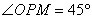

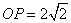
由余弦定理得,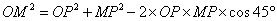
得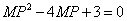
解得
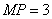
(2)设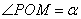
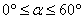
在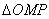
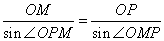
所以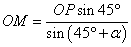
同理
故
因为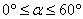
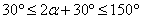
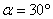
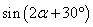
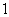
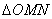
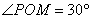


知识点
在△ABC中,a=3,b=5,sin A=
正确答案
解析
根据正弦定理,


知识点
在△ABC中,角A,B,C所对的边分别为a,b,c,已知A=

正确答案

解析
∵在△ABC中,A=

∴由正弦定理




∵a<b,∴A<B,
∴B=

知识点
四边形ABCD的内角A与C互补,AB=1,BC=3,CD=DA=2。
(1)求C和BD;
(2)求四边形ABCD的面积。
正确答案
(1)C=60°,BD=
(2)2
解析
(1)在△BCD中,BC=3,CD=2,
由余弦定理得:BD2=BC2+CD2﹣2BC•CDcosC=13﹣12cosC①,
在△ABD中,AB=1,DA=2,A+C=π,
由余弦定理得:BD2=AB2+AD2﹣2AB•ADcosA=5﹣4cosA=5+4cosC②,
由①②得:cosC=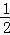
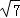
(2)∵cosC=

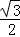
则S=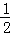
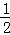
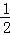
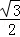
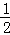
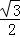
知识点
在



正确答案
解析
由












知识点
在锐角△ABC中,内角A,B,C的对边分别为a,b,c,且2asin B=
(1)求角A的大小;
(2)若a=6,b+c=8,求△ABC的面积。
正确答案
(1)
解析
(1)由2asin B=


因为A是锐角,所以
(2)由余弦定理a2=b2+c2-2bccos A,得b2+c2-bc=36.
又b+c=8,所以
由三角形面积公式S=
知识点
扫码查看完整答案与解析