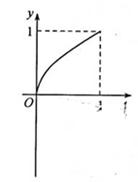已知某试验范围为[10,90],若用分数法进行4次优选试验,则第二次试点可以是 。
正确答案
40或60(只填一个也正确)
解析
有区间长度为80,可以将其等分8段,利用分数法选取试点:

知识点
为了了解2013年某校高三学生的视力情况,随机抽查了一部分学生视力,将调查结果分组,分组区间为


(1)求频率分布表中未知量
(2)从样本中视力在

正确答案
见解析。
解析
(1)由表可知,样本容量为n,
由(5.1,5.4]一组频数为2,频率为0.04,则
由
y=50﹣3﹣6﹣25﹣2=14,
(2)设样本视力在(3.9,4.2]的3人为a,b,c;样本视力在(5.1,5.4]的2人为d,e。
由题意从5人中任取两人的基本事件空间为:Ω={(a,d),(a,e),(b,d),(b,e),(c,d),(c,e),(a,b),(a,c),(b,c),(d,e)},共10个基本事件;
设事件A表示“抽取的两人的视力差的绝对值低于0.5”,则事件A包含的基本事件有:(a,b),(a,c),(b,c),(d,e),共4个基本事件;
P(A)=

故抽取的两人的视力差的绝对值低于0.5的概率为
知识点
一个高为2的圆柱,底面周长为
正确答案
解析
根据该圆柱的底面周长得底面圆的半径为

知识点
在△ABC中,角A,B,C的对边分别为a,b,c.已知3cos(B-C)-1=6cos Bcos C。
(1)求cos A;
(2)若a=3,△ABC的面积为
正确答案
(1) 

解析
(1)由3cos(B-C)-1=6cos Bcos C,
得3(cos Bcos C-sin Bsin C)=-1,
即cos(B+C)=

(2)由于0<A<π,cos A=

又S△ABC=

由余弦定理a2=b2+c2-2bccos A,得b2+c2=13.
解方程组

知识点
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:
①sin213°+cos217°-sin13°cos17°;
②sin215°+cos215°-sin15°cos15°;
③sin218°+cos212°-sin18°cos12°;
④sin2(-18°)+cos248°-sin(-18°)cos48°;
⑤sin2(-25°)+cos255°-sin(-25°)cos55°。
(1)试从上述五个式子中选择一个,求出这个常数;
(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论。
正确答案
见解析
解析
方法一:(1)选择②式,计算如下:
sin215°+cos215°-sin15°cos15°=1-

(2)三角恒等式为sin2α+cos2(30°-α)-sinα·cos(30°-α)=
证明如下:
sin2α+cos2(30°-α)-sinαcos(30°-α)
=sin2α+(cos30°cosα+sin30°sinα)2-sinα·(cos30°cosα+sin30°sinα)
=sin2α+




=


方法二:(1)同方法一。
(2)三角恒等式为sin2α+cos2(30°-α)-sinα·cos(30°-α)=
证明如下:
sin2α+cos2(30°-α)-sinαcos(30°-α)
=
=





=






=
知识点
如图,直四棱柱ABCD – A1B1C1D1中,AB//CD,AD⊥AB,AB=2,AD=
(1)证明:BE⊥平面BB1C1C;
(2)求点B1 到平面EA1C1 的距离
正确答案
见解析
解析
(1)证明:过B作CD的垂线交CD于F,则
在
在
由
(2)

同理,
因此


知识点
已知函数
(1) 求
(2) 求

正确答案
(1) 
解析
(1)因为



(2)因为




知识点
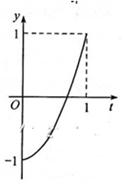
如图。已知l1⊥l2,圆心在l1上、半径为1m的圆O在t=0时与l2相切于点A,圆O沿l1以1m/s的速度匀速向上移动,圆被直线l2所截上方圆弧长记为x,令y=cosx,则y与时间t(0≤x≤1,单位:s)的函数y=f(t)的图像大致为
正确答案
解析
法1:取特值x=0时t=0,则y=1排除A,D,取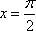
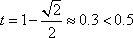
法2:依题意可知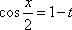
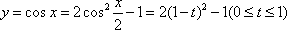
知识点
若数列


正确答案
4
解析
略
知识点
在△ABC中,角A,B,C的对边分别为a,b,c,已知
且C=120°。
(1)求角A;
(2)若a=2,求c。
正确答案
见解析
解析
(1)由正弦定理,

所以
因为
所以


(2)由(1)知,

所以
知识点
扫码查看完整答案与解析