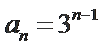- 交、并、补集的混合运算
- 共98题
2.设全集



正确答案
解析
∵

考查方向
解题思路
先算出补集,然后求交集
易错点
求集合的交集和补集时错误
知识点
记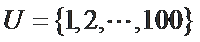
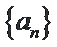

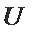
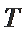
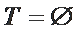
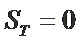
若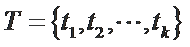
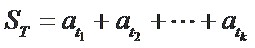
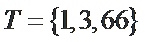
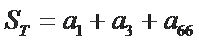
现设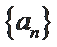

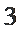
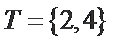
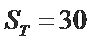
27.求数列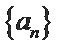
28.对任意正整数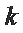
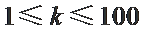
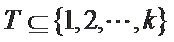
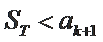
29.设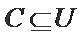
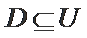
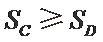
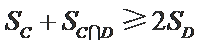
正确答案
解析
当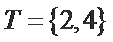
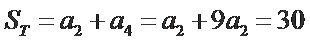
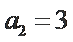
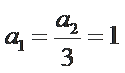
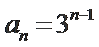
考查方向
解题思路
易错点
放缩,数列基本关系的转化,等比数列求和的应用
正确答案
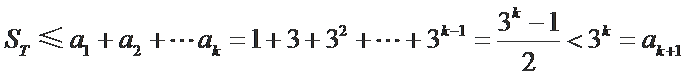
解析
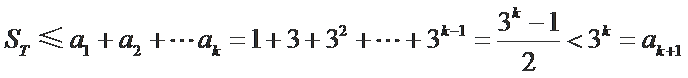
考查方向
解题思路
易错点
放缩,数列基本关系的转化,等比数列求和的应用
正确答案
设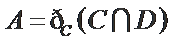
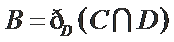
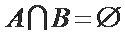
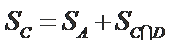
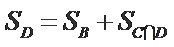
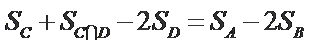
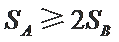
由条件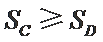
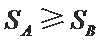
① 若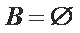
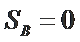
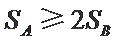
② 若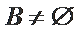
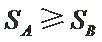
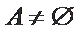
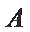
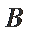
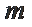
若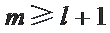
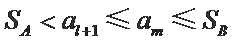
因为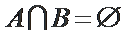
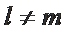
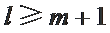
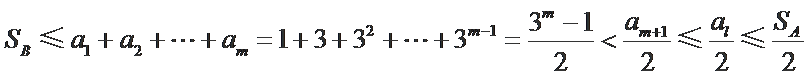
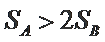
综上所述,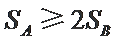
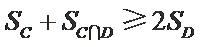
解析
设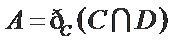
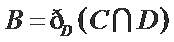
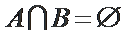
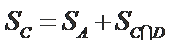
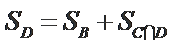
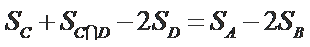
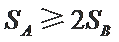
由条件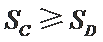
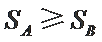
① 若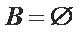
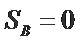
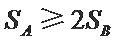
② 若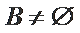
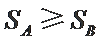
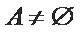
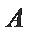
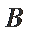
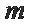
若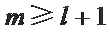
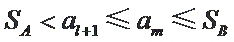
因为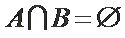
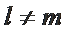
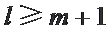
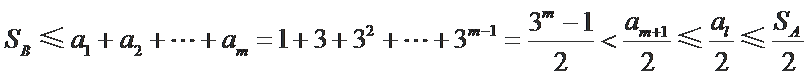
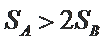
综上所述,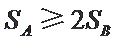
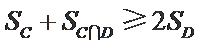
考查方向
解题思路
易错点
放缩,数列基本关系的转化,等比数列求和的应用
2.设全集



正确答案
解析
因为



所以
考查方向
解题思路
研究两集合的关系时,关键是将两集合的关系转化为元素间的关系,本题实质求满足属于集合A或不属于集合B的元素的集合.
易错点
研究集合问题,一定要抓住元素,看元素应满足的属性.
知识点
11.已知集合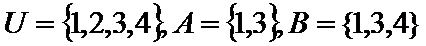
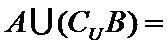
正确答案
{1,2,3}
解析
由题意得,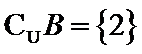
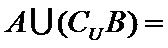
考查方向
解题思路
先求出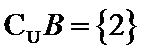
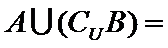
易错点
马虎出错。
知识点
1.已知集合



正确答案
解析
由



考查方向
解题思路
先分别求出两个集合中代表元素的取值范围,再求交集。
易错点
集合Q中不等式解错导致出错。
知识点
1.已知全集



正确答案
解析
易知

考查方向
解题思路
先求集合B在全集U中的补集,再求交集。
易错点
忽略集合中元素的互异性导致出错。
知识点
1.设集合
正确答案
解析


考查方向
解题思路
求出A集合,然后计算出两个集合的交集。
易错点
A集合取反。
知识点
1.已知全集



正确答案
解析
因为



考查方向
解题思路
根据题意,先确定集合A和B表示的x的范围,然后在求交集和补集
易错点
集合的基本概念理解不透彻
知识点
1.已知集合A={x|x≥4},B={x|-1≤2x-1≤0},则CRA∩B=
正确答案
解析
考查方向
解题思路
本题属于简单题,可使用数轴表示出集合直接判断,
易错点
该题主要易错于对端点情况的判断错误
知识点
1.设集合

正确答案
解析
由补集的概念,得
考查方向
解题思路
求补集的运算和并的运算即可
易错点
对补集的运算和并的运算出现错误
知识点
扫码查看完整答案与解析