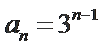- 交、并、补集的混合运算
- 共98题
1
题型:
单选题
|
2.设全集



正确答案
B
解析
∵

考查方向
本题主要是考查了集合的交集、补集运算.
解题思路
先算出补集,然后求交集
易错点
求集合的交集和补集时错误
知识点
交、并、补集的混合运算
1
题型:简答题
|
记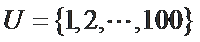
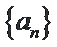

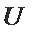
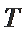
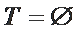
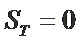
若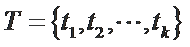
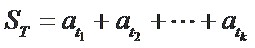
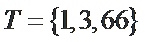
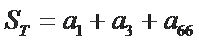
现设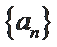

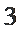
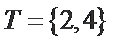
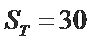
27.求数列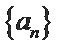
28.对任意正整数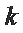
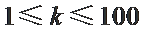
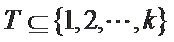
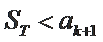
29.设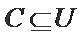
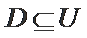
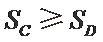
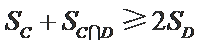
第(1)小题正确答案及相关解析
正确答案
解析
当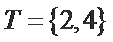
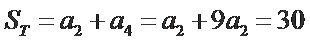
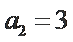
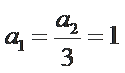
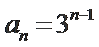
考查方向
等比数列的通项公式、求和
解题思路
易错点
放缩,数列基本关系的转化,等比数列求和的应用
第(2)小题正确答案及相关解析
正确答案
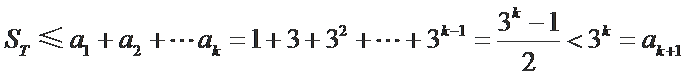
解析
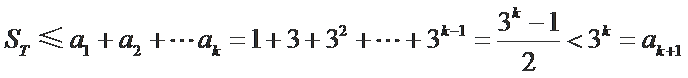
考查方向
等比数列的通项公式、求和
解题思路
易错点
放缩,数列基本关系的转化,等比数列求和的应用
第(3)小题正确答案及相关解析
正确答案
设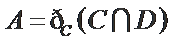
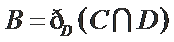
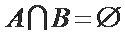
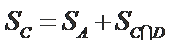
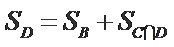
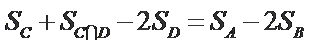
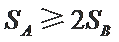
由条件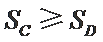
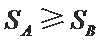
① 若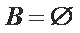
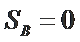
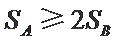
② 若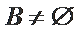
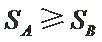
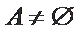
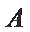
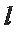
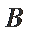
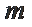
若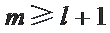
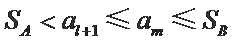
因为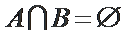
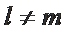
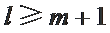
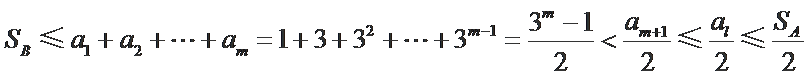
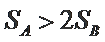
综上所述,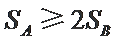
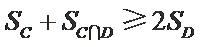
解析
设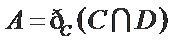
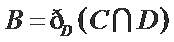
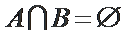
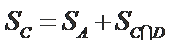
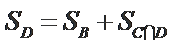
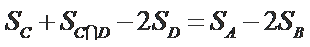
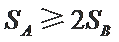
由条件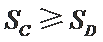
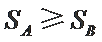
① 若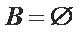
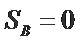
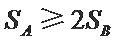
② 若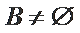
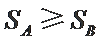
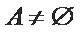
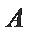
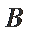
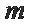
若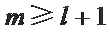
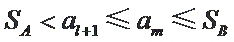
因为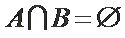
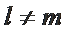
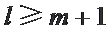
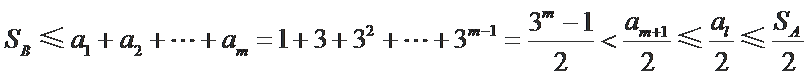
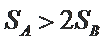
综上所述,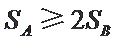
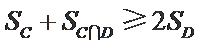
考查方向
等比数列的通项公式、求和
解题思路
易错点
放缩,数列基本关系的转化,等比数列求和的应用
1
题型:填空题
|
2.设全集



正确答案
解析
因为



所以
考查方向
本题考查集合的交、并、补的混合运算,熟练掌握集合的交并补的运算规则是解本题的关键.本题考查了推理判断的能力.
解题思路
研究两集合的关系时,关键是将两集合的关系转化为元素间的关系,本题实质求满足属于集合A或不属于集合B的元素的集合.
易错点
研究集合问题,一定要抓住元素,看元素应满足的属性.
知识点
交、并、补集的混合运算
1
题型:填空题
|
11.已知集合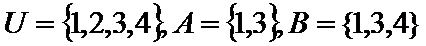
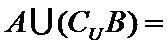
正确答案
{1,2,3}
解析
由题意得,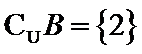
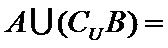
考查方向
本题主要考察集合间的运算,意在考察考生对于基础知识的掌握程度。
解题思路
先求出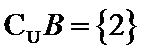
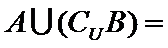
易错点
马虎出错。
知识点
交、并、补集的混合运算
1
题型:
单选题
|
1.设集合

正确答案
C
解析
由补集的概念,得
考查方向
本题主要考查了补集的运算和并的运算等知识,为高考题的必考题,在近几年的各省高考题出现的频率较高
解题思路
求补集的运算和并的运算即可
易错点
对补集的运算和并的运算出现错误
知识点
交、并、补集的混合运算
下一知识点 : Venn图表达集合的关系及运算
扫码查看完整答案与解析