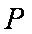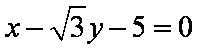- 直线与圆相交的性质
- 共61题
已知,圆C:


(1)当a为何值时,直线
(2)当直线


正确答案
见解析。
解析
解:将圆C的方程

(1) 若直线

解得
(2) 解法一:过圆心C作CD⊥AB,
则根据题意和圆的性质,得
解得
(解法二:联立方程


设此方程的两根分别为


∴直线


知识点
已知曲线
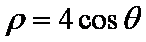
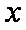

(1)求曲线
(2)设曲线



正确答案
(1)
(2)S=
解析
(1)对于
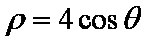
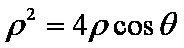
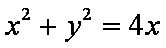
对于:由
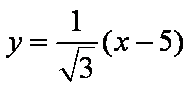
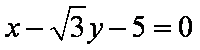
(2)由(1)可知
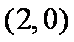
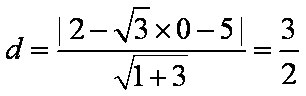
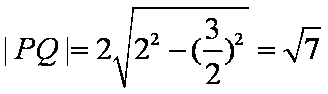
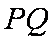

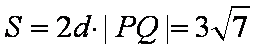
知识点
在平面直角坐标系xOy中,已知点P(3,0)在圆C:x2+y2﹣2mx﹣4y+m2﹣28=0内,动直线AB过点P且交圆C于A,B两点,若△ABC的面积的最大值为16,则实数m的取值范围为 。
正确答案
(3﹣2



解析
圆的标准方程为(x﹣m)2+(y﹣2)2=32,
则圆心C(m,2),半径r=4
S△ABC=
∴当∠ACB=90时S取最大值16,
此时△ABC为等腰直角三角形,AB=
则C到AB距离=
∴4≤PC<4
即4≤

∴16≤(m﹣3)2+4<32,
即12≤(m﹣3)2<28,
∴
解得3﹣2



知识点
在直角坐标系


(



程是
(1)将圆
(2)若直线



正确答案
见解析
解析
(1)∵
∴ 

∴圆

圆心的直角坐标为

(2)直线


代入圆

设


∴
知识点
直线l:y=kx+1与圆O:x2+y2=1相交于A,B两点,则“k=1”是“
正确答案
解析
略
知识点
扫码查看完整答案与解析