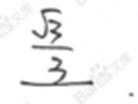- 简单空间图形的三视图
- 共120题
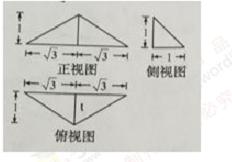
12.已知某三菱锥的三视图如图所示，
则该三菱锥的体积 。
正确答案
知识点
如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为( )
正确答案
知识点
9.一个几何体的三视图如图所示,其中正视图是正三角形,则几何体的外接球的体积为( )
A
B
C
D
正确答案
解析
此几何体是三棱锥P-ABC（直观图如右图）,底面是斜边长为4的等腰直角三角形ACB,且顶点在底面内的射影D是底面直角三角形斜边AB的中点.易知,三棱锥P-ABC的外接球的球心O在PD上.
设球O的半径为r,则
∴外接球的表面积为
考查方向
解题思路
先将直观图还原出来，再计算球的半径进一步计算出球的表面积。
易错点
不会还原直观图。
知识点
11.圆柱被一个平面截去一部分后与半球（半径为r）组成一个几何体，该几何体三视图中的正视图和俯视图如图所示，若该几何体的表面积为16+20π，则r=( )
正确答案
知识点
7.一个几何体的三视图如图所示，且其侧（左）视图是一个等边三角形，则这个几何体的体积为（ ）
A
B
C
D
正确答案
解析
由三视图可知该几何体为一个三棱锥和一个四棱锥的组合体，其中高均为
考查方向
解题思路
1、将几何体放到长方体中考虑；
2、得到原来的几何体后求出其体积即可。
易错点
1.无法根据三视图还原成直观图；
2.不会计算得到几何体的体积。
知识点
9．如图是正三棱锥V－ABC的正视图、侧视图和俯视图，则其侧视图的面积是
正确答案
解析
如图计算底面高
体高
所以侧面积
考查方向
解题思路
1）根据三视图得出底边长为
2）计算体高VA,得出结果
易错点
主要易错于读错数据
知识点
6.—个长方体被一个平面截去一部分后所剩几何体的三视图如下图所示（单位：cm)，则该几何体的体积为
A120cm3
B80cm3
C100cm3
D60cm3
正确答案
解析
由三视图可判断几何体为一长方体削去一个角，其直观图如图：
长方体的长、宽、高分别为5、4、6，
∴长方体的体积为5×4×6=120，削去的三棱锥的体积为5×4×6=20，
∴该几何体的体积为120-20=100cm2．
故选C
考查方向
本题主要考查空间几何体的三视图，根据三视图还原成空间几何体求体积，中档题，体现了学生对所学知识的运用能力。
易错点
三视图概念不清楚
知识点
8．如图，网格纸是边长为1的小正方形，在其上用粗线画出了某多面体的三视图，则该多面体的体积为（ ）
正确答案
解析
由图可知，此多面体是一个以4为高，以长和宽分别是6、2的矩形为底的四棱锥。则V=sh/3=16。A选项不正确，B选项不正确，D选项不正确，所以选C选项。
考查方向
本题主要考查三视图
解题思路
（1）还原几何体；（2）求出体积，即可得到结果。
A选项不正确，B选项不正确，D选项不正确，所以选C选项。
易错点
本题易在还原几何体时发生错误。
知识点
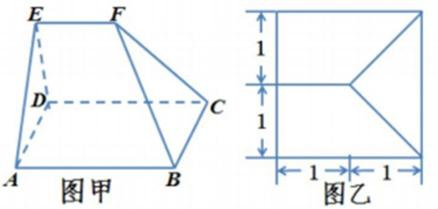
16. 多面体ABCDEF(如图甲)的俯视图如图乙，己知面ADE为正三角形．
（1）求多面体ABCDEF的体积；
（2）求证：平面ACF⊥平面BDF．
正确答案
（1）
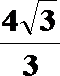
（2）略．
解析
试题分析：本题属于立体几何中的基本问题，题目的难度是逐渐由易到难．
(1)分别取AB、CD的中点M、N，连接EM、EN、MN，多面体体积转化为棱柱AED-MFN的体积V1与四棱锥F-MBCN的体积V2之和。
由三视图可知，AD=2，AM=DN=1，面ADE为正三角形且垂直于底面ABCD，知F点到底面的距离为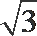
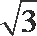
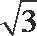
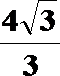
考查方向
本题考查了立体几何中的体积和面面垂直的问题．属于高考中的高频考点。
解题思路
本题考查立体几何中的体积和面面垂直的问题，解题步骤如下：
（1）做辅助线，拆分多面体。
（2）转化为证明线面垂直。
易错点
（1）第一问中的多面体的拆分。
（2）第二问中的面面垂直的转化。。
知识点
9．某几何体的三视图如下图所示，则该几何体中，面积最大的侧面的面积为（ ）
A
B
C
D
正确答案
解析
由三视图可知，几何体的直观图如图所示，
平面AED⊥平面BCDE，四棱锥A-BCDE的高为1，四边形BCDE是边长为1的正方形，
则
考查方向
本题主要考查了三视图和侧面积
解题思路
先通过三视图得出几何体是四棱锥，并且平面AED⊥平面BCDE，四棱锥A-BCDE的高为1，四边形BCDE是边长为1的正方形，然后分别求出四个侧面积进行比较
易错点
本题易在几何体的直观图看不懂，平面AED⊥平面BCDE，四棱锥A-BCDE的高为1，四边形BCDE是边长为1的正方形
知识点
扫码查看完整答案与解析