- 等比数列的性质及应用
- 共160题
10. 已知数列




正确答案
解析
由










A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
解题思路
由等差数列等比数列的性质,把

作差法比较大小。
易错点
等差等比数列性质不熟悉,没有发现第


转化思想,没想到把

知识点
已知等比数列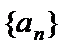
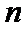
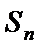
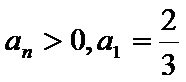
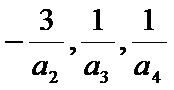
22.求数列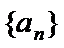
23.设数列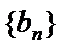
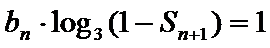
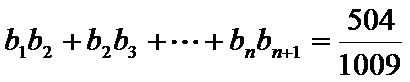
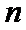
正确答案
(Ⅰ)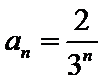
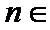

解析
(Ⅰ)设等比数列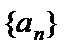
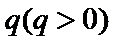
∵ 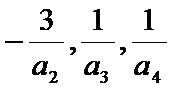
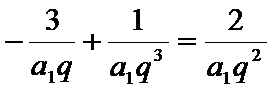
∴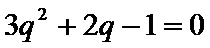
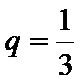
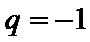
∴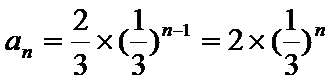
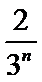
∴数列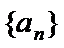
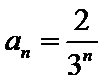
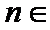

考查方向
解题思路
先根据题中给出的条件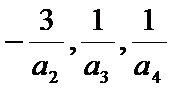
易错点
对于题中给出的条件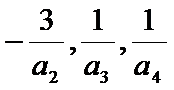
正确答案
(Ⅱ)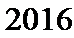
解析
(Ⅱ)由(Ⅰ)知,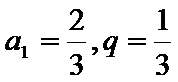
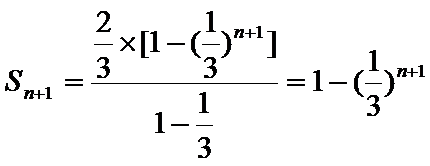
∵数列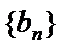
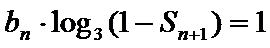
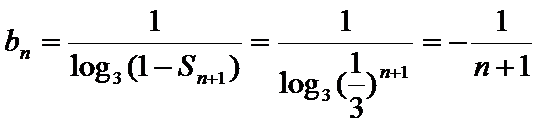
∴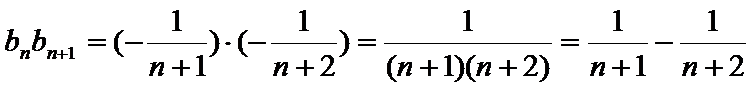
∴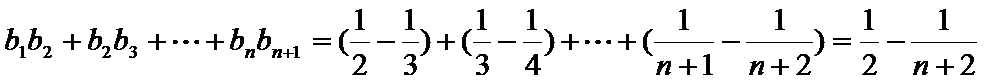
由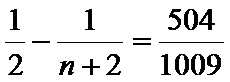
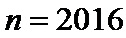
∴满足方程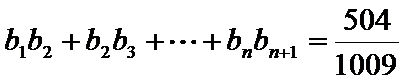
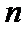
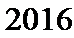
考查方向
解题思路
1.先根据题中给出的条件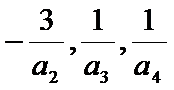
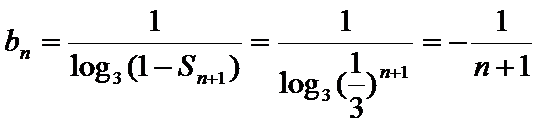
易错点
1.对于题中给出的条件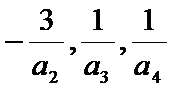
16. 设








正确答案
解析
f(
























考查方向
解题思路
可利用倒序相加求
易错点
求

知识点
11.已知递增的等差数列







正确答案


解析
故此题答案为

考查方向
解题思路
先根据



易错点
本题易在求和项数的判断上出现错误。
知识点
9.已知数列




的前

正确答案
解析
由




考查方向
解题思路
先判断出该数列是一个等差数列,然后再求最值。
易错点
不会转化来做。
知识点
扫码查看完整答案与解析



















