- 等比数列的性质及应用
- 共160题
在无穷数列








(1)设数列








(2)若


(3)若

正确答案
见解析
解析
(1)解:


(2)解:因为


所以
因为使得


所以





所以
(3)解:由题意,得
结合条件

又因为使得





所以

设

假设

则当



所以

因为
所以公差
所以

这与
所以
又因为
所以
由


因为使得


所以
由

知识点
已知数列




(1)求证: 数列
(2)设



(3)问是否存在常数



正确答案
见解析。
解析
(1)∵an,an+1是关于x的方程
∴
∵
故数列

(2)解:由(1)得
∴
=
因此,
要使bn>λSn,对∀n∈N*都成立,
即
①当n为正奇数时,由(*)式得:
即
∵2n+1﹣1>0,∴
因为
②当n为正偶数时,由(*)式得:
∵2n﹣1>0,∴
∵


∴存在常数λ,使得bn>λSn对∀n∈N*都成立时λ的取值范围为(﹣∞,1)
知识点
过双曲线




正确答案
解析
略
知识点
若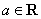
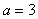
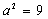
正确答案
解析
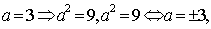
知识点
定义:若各项为正实数的数列


已知数列




(1)试判断数列
(2)记


(3)若数列





正确答案
(1)数列

解析
(1)答:数列
理由:



又
∴
∴数列
证明(2) 

又





(3)由题意可知,无穷等比数列



化简,得
若


又




知识点
扫码查看完整答案与解析














