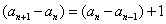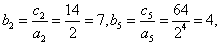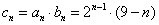- 等比数列的性质及应用
- 共160题
已知等比数列{an}的公比q<0,其前n项和为Sn,则

正确答案
解析
知识点
已知函数


(1)求证:数列
(2) 设



正确答案
见解析。
解析
(1)证:由题意


∴数列


(2) 解:由(1)知,
∴

②-①,得
∴.
因为


知识点
在ABC中,角A、B、C的对边分别为a、b、c,已知
(1)求
(2)若

正确答案
见解析。
解析
(1)由a、b、c成等比数列,得
由正弦定理,得
所以
(2)由

又

所以
由余弦定理,得
代入数值,得

知识点
已知在数列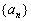


(1)求证:数列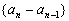
(2)求数列
正确答案
见解析。
解析
(1)证明:由

所以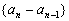

(2)解:由(1)知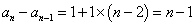
所以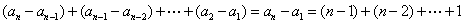
所以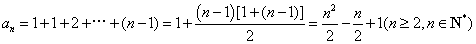
因为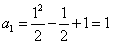
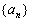
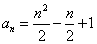
知识点
给出下列四个函数:




正确答案
解析
略
知识点
若函数


(1)判断下列函数:①

(2)证明:函数
(3)判断函数
正确答案
见解析
解析
(1)①②都是等比源函数;
(2)证明: 

因为
所以函数
其他的数据也可以
(3)函数
证明如下:
假设存在正整数




等式两边同除以

因为
所以等式
所以假设不成立,说明函数
知识点
已知首项


正确答案
解析
(探究性理解水平/数列的极限、等比数列的前









知识点
设等比数列{

(1)求数列{
(2)在

(I)在数列{

(II)求证:
正确答案
见解析。
解析
(1)由
可得:
两式相减:
又
因为数列


所以
(2)由(1)可知
因为:

(Ⅰ)假设在数列


则:


因为

(*)可以化简为

所以在数列


(Ⅱ)令

两式相减:

知识点
已知





正确答案
70
解析
略
知识点
已知数列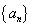
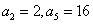

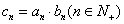
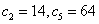
(1)求数列
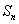
(2)求数列
(3)记数列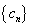
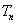
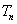
正确答案
见解析。
解析
解:(1)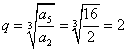

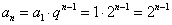
(2)因为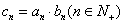
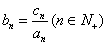
所以

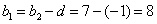
(3)因为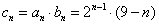

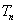
故
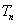
又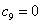

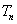
知识点
扫码查看完整答案与解析