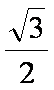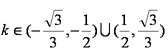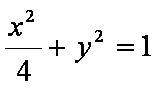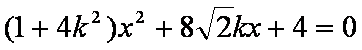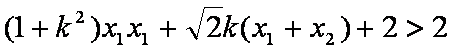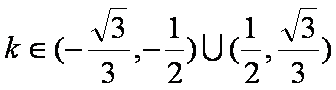- 等比数列的性质及应用
- 共160题
设同时满足条件:①












(1)求
(2)设



正确答案
见解析。
解析
(1)因为
当




∴
(2)由(1)知,
若



故

再将


由于①
(或做差更简单:因为

②

所以符合①②,故
知识点
已知数列






(1)求数列 



(2)若对任意的 


(3)是否存在正整数m,n 

的值;若不存在,请说明理由.
正确答案
见解析
解析
(1)(法一)在


得
解得

又





(法二)

由

又


(
(2)①当







②当










综合①、②可得

(3)
若

即
由



又



因此,当且仅当



[另解:因为



知识点
已知等差数列{an}的首项a1=2,a7=4a3,前n项和为Sn。
(1) 求an及Sn;
(2) 设bn=
正确答案
见解析
解析
(1)设公差为d,
由题意知a1+6d=4(a1+2d),
由a1=2解得d=-3,
故an=-3n+5, Sn=
(2) 由(1)得bn=



由基本不等式得n+

所以bn=




从而得bn的最大值为
知识点
已知公差不为零的等差数列


(1)求数列
(2)令




正确答案
见解析。
解析
(1)设数列


解得:



(2)
知识点
已知中心在原点的椭圆
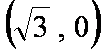
(1)求椭圆
(2)若直线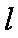
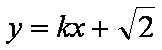

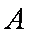
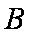
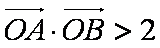
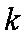
正确答案
(1)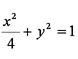
解析
解析:(1)椭圆
(2)
由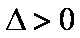
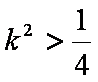


由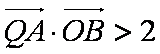
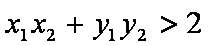
解得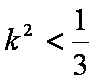
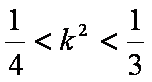
知识点
已知数列

(1)求
(2)求数列
(3)设数列

正确答案
见解析。
解析
(1)解:由

(2)由
∴数列{

(3)

①-②得
则

即当n=1或2时,
知识点
设正项等比数列{an}的首项
(1)求{an}的通项;
(2)求{nSn}的前n项和Tn。
正确答案
见解析
解析
(1)由210S30﹣(210+1)S20+S10=0得210(S30﹣S20)=S20﹣S10,
即210(a21+a22+…+a30)=a11+a12+…+a20,
可得210•q10(a11+a12+…+a20)=a11+a12+…+a20。
因为an>0,所以210q10=1,解得
(2)由题意知
则数列{nSn}的前n项和
前两式相减,得

知识点
设公比不为1的等比数列{an}满足:a1,a3,a2成等差数列。
(1)求公比q的值;
(2)证明:
正确答案
见解析。
解析
(1)

(2)

∴
知识点
18.设
(1)求
(2)设


正确答案
见解析
解析
解析:(1)由
解之得q=2(q=-1舍去)
∴
(2)

∴
∴
下式减去上式得
知识点
已知实数




正确答案
解析
略
知识点
扫码查看完整答案与解析