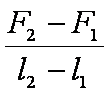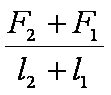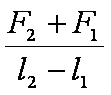- 胡克定律
- 共30题
一根轻质弹簧一端固定,用大小为F1的力压弹簧的另一端,平衡时长度为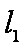
正确答案
解析
略
知识点
如图,用橡皮筋将一小球悬挂在小车的架子上,系绕处于平衡状态。现使小车从静止开始向左加速,加速度从零开始逐渐增大到某一值,然后保持此值,小球稳定地偏离竖直方向某一角度(橡皮筋在弹性限度内)。与稳定在竖直位置时相比,小球的高度 ( )
正确答案
解析
略
知识点
14.下列说法正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.(16分)一转动装置如图所示,四根轻杆OA、OC、AB和CB与两小球以及一小环通过铰链连接,轻杆长均为l,球和环的质量均为m,O端固定在竖直的轻质转轴上,套在转轴上的轻质弹簧连接在O与小环之间,原长为L,装置静止时,弹簧长为
(1)弹簧的劲度系数k;
(2)AB杆中弹力为零时,装置转动的角速度
(3)弹簧长度从

正确答案
(1)装置静止时,设





小环受到弹簧的弹力
小环受力平衡
小球受力平衡
解得
(2)设






小环受到弹簧的弹力
小环受力平衡 
对小球

解得
(3)弹簧长度为






小环受到弹簧的弹力
小环受力平衡
对小球
解得
整个过程弹簧弹性势能变化为零,则弹力做的功为零,由动能定理
解得
解析
解析已在路上飞奔,马上就到!
知识点
如图所示,质量为






(1)求物块处于平衡位置时弹簧的长度;
(2)选物块的平衡位置为坐标原点,沿斜面向下为正方向建立坐标轴,用
(3)求弹簧的最大伸长量;
(4)为使斜面始终处于静止状态,动摩擦因数
正确答案
见解析
解析
(1)设物块在斜面上平衡时,弹簧伸长量为x,有


(2)由物块所受
得 :
解得:
符合简谐振动的回复力特征,所以是简谐振动.
(3)物块做简谐振动的振幅为

(4)物块运动时,要斜面静止则需要
在物块具有最大向上加速度时保持不动,则整个过程保持不动
联立求解得:
知识点
某学习小组要研究影响弹簧劲度系数的因素,他们猜想弹簧的劲度系数k可能与制成弹簧的钢丝的半径r、弹簧圈的半径R和弹簧的圈数n有关。为此他们选择了同种材料制成的不同粗细的钢丝,分别绕成了弹簧圈半径不同的弹簧。再利用薄铁片做为卡片和指示弹簧被拉伸后所到位置的指针,用这个卡片选择对弹簧的不同位置施力,实现对同一个弹簧使用圈数的改变(如图5甲所示),从而可得到圈数不同的弹簧。他们分别研究了k与r、k与R和k与n的关系(在研究k与弹簧的一个参量的关系时,另外两参量保持不变),并根据测得的数据,分别画出了k-r、k-R和k-n图象(如图5乙、丙、丁所示)。
关于上面实验所采用的科学方法,以及k与r、R和n的关系,下列说法中可能正确的是 ( )
正确答案
解析
略
知识点
如图所示,用完全相同的轻弹簧A、B、C将两个相同的小球连接并悬挂,小球处于静止状态,弹簧A与竖直方向的夹角为30o,弹簧C水平,则弹簧A、C的伸长量之比为
正确答案
解析
略
知识点
蹦床比赛分成预备运动和比赛动作。最初,运动员静止站在蹦床上在预备运动阶段,他经过若干次蹦跳,逐渐增加上升高度,最终达到完成比赛动作所需的高度;此后,进入比赛动作阶段。
把蹦床简化为一个竖直放置的轻弹簧,弹力大小F=kx (x为床面下沉的距离,k为常量)。质量m=50kg的运动员静止站在蹦床上,床面下沉x0=0.10m;在预备运动中,家丁运动员所做的总共W全部用于其机械能;在比赛动作中,把该运动员视作质点,其每次离开床面做竖直上抛运动的腾空时间均为△t=2.0s,设运动员每次落下使床面压缩的最大深度均为xl。取重力加速度g=I0m/s2,忽略空气阻力的影响。
(1)求常量k,并在图中画出弹力F随x变化的示意图;
(2)求在比赛动作中,运动员离开床面后上升的最大高度hm;
(3)借助F-x 图像可以确定弹性做功的规律,在此基础上,求 x1 和W的值
正确答案
答案:见解析
解析
(1)床面下沉
有

F-x图线如图所示。
(2)运动员从x=0处离开床面,开始腾空,由运动的对称性知其上升、下落的时间相等,


(3)参照由速度时间图线求位移的方法可知F-x图线下的面积等于弹力做的功,从x处到x=0处,弹力做的功
运动员从



对整个预备运动过程分析,由题设条件以及功和能的关系,有
解得W=2525J.
知识点
如图所示,倾角为α,质量为mC的斜面体C放在粗糙的水平地面上。质量分别为mA、mB的物体A和B通过劲度系数为k的轻弹簧连接后放在光滑斜面上,对B施加一个与斜面成β角斜向上的拉力,使A、B、C均处于静止状态(B未离开斜面).重力加速度为g。下列说法正确的是( )
正确答案
解析
A:把ABC看成一个整体,整体处于平衡状态,合力为零,则竖直方向有:FN+Fsin(α+β)=(mA+mB+mC)g,解得:FN=(mA+mB+mC)g﹣Fsin(α+β),根据牛顿第三定律可知,斜面体对地面的压力大小为(mA+mB+mC)g﹣Fsin(α+β)<(mA+mB+mC)g,故A错误;
B:ABC整体水平方向受力平衡,则斜面体受到地面对斜面体水平向左的摩擦力与F在水平方向上的分量相等,故B错误;
C:对A受力分析,受到重力,支持力和弹簧拉力作用,受力平衡,合力为零,则F弹=mgsinα,根据胡克定律得:F弹=kx,则x=
D:对AB受力分析,受到重力,支持力和拉力作用,受力平衡,合力为零,则(mA+mB)gsinα=Fcosβ,解得:F=
知识点
8.如图,物块a、b和c的质量相同,a和b、b和c之间用完全相同的轻弹簧S1和S2相连,通过系在a上的细线悬挂于固定点O;整个系统处于静止状态;现将细绳剪断,将物块a的加速度记为a1,S1和S2相对原长的伸长分别为△l1和△l2,重力加速度大小为g,在剪断瞬间( )
A.a1=3g
B.a1=0
C. △l1=2△l2
D. △l1=△l2
正确答案
A;C
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析