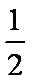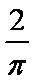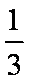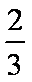- 随机事件及其概率
- 共412题
甲、乙两人玩掷骰子游戏:甲先掷一个骰子,记下向上的点数;然后乙再掷,同样记下向上的点数.如果两人所掷点数之和为偶数则甲胜,否则乙获胜。
(1)求甲胜且点数之和为6的事件发生的概率;
(2)这种游戏规则公平吗?用你所学的知识说明理由。
正确答案
见解析。
解析
(1)设“甲胜且点数的和为6”为事件

则
两人掷骰子的结果包括(1,1),(1,2),…,(1,5),(1,6),(2,1),…,(6,1),…,(6,6)共36个基本事件;
事件
所以
所以,甲胜且点数之和为6的概率为
(2)这种游戏公平。
设“甲胜”为事件B,“乙胜”为事件C.甲胜即两个点数的和为偶数.
所包含基本事件为以下18个:(1,1),(1,3),(1,5),(2,2),(2,4),(2,6),(3,1),(3,3),(3,5),(4,2),(4,4),(4,6),(5,1),(5,3)(5,5),(6,2),(6,4),(6,6)
所以甲胜的概率为
乙胜的概率为
所以这种游戏是公平的
知识点
甲、乙两校各有3名教师报名支教,期中甲校2男1女,乙校1男2女。
(1)若从甲校和乙校报名的教师中各任选1名,写出所有可能的结果,并求选出的2名教师性别相同的概率;
(2)若从报名的6名教师中任选2名,写出所有可能的结果,并求选出的2名教师来自同一学校的概率。
正确答案
见解析。
解析
甲校的男教师用A、B表示,女教师用C表示,乙校的男教师用D表示,女教师用E、F表示,
(1)根据题意,从甲校和乙校报名的教师中各任选1名,
有(AD),(AE),(AF),(BD),(BE),(BF),(CD),(CE),(CF),共9种;
其中性别相同的有(AD)(BD)(CE)(CF)四种;
则选出的2名教师性别相同的概率为P=
(2)若从报名的6名教师中任选2名,
有(AB)(AC)(AD)(AE)(AF)(BC)(BD)(BE)(BF)(CD)(CE)(CF)(DE)(DF)(EF)共15种;
其中选出的教师来自同一个学校的有6种;
则选出的2名教师来自同一学校的概率为P=
知识点
某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
(1)写出表中①②位置的数据;
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率,
正确答案
见解析。
解析
(1)①②位置的数据分别为12、0.3;
(2) 第三、四、五组参加考核人数分别为3、2、1;
(3)设上述6人为abcdef(其中第四组的两人分别为d,e),则从6人中任取2人的所有情形为:{ab,ac,ad,ae,af,bc,bd,be,bf,cd,ce,cf,de,df,ef}共有15种,
记“2人中至少有一名是第四组”为事件A,则事件A所含的基本事件的种数有9种,
所以

知识点
某城市有甲、乙、丙3个旅游景点,一位客人游览这三个景点的概率分别是0.4,0.5,0.6,且客人是否游览哪个景点互不影响,设ξ表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值。
(1)求ξ的分布及数学期望;
(2)记“函数f(x)=x2﹣3ξx+1在区间[2,+∞)上单调递增”为事件A,求事件A的概率。
正确答案
见解析
解析
(1)分别记“客人游览甲景点”,“客人游览乙景点”,“客人游览丙景点”
为事件A1,A2,A3。
由已知A1,A2,A3相互独立,P(A1)=0.4,P(A2)=0.5,P(A3)=0.6。
客人游览的景点数的可能取值为0,1,2,3.相应地,客人没有游览的景点数的可能取值
为3,2,1,0,所以ξ的可能取值为1,3。
P(ξ=3)=P(A1•A2•A3)+P(
=P(A1)P(A2)P(A3)+P(
=2×0.4×0.5×0.6=0.24,
P(ξ=1)=1﹣0.24=0.76。
所以ξ的分布列为
Eξ=1×0.76+3×0.24=1.48。
(2)因为
所以函数
要使f(x)在[2,+∞)上单调递增,当且仅当
从而
知识点
已知某种从太空飞船中带回的植物种子每粒成功发芽的概率都为
(1)第一小组做了三次实验,求至少两次实验成功的概率;
(2)第二小组进行试验,到成功了4次为止,求在第四次成功之前共有三次失败,且恰有两次连续失败的概率。
正确答案
见解析
解析
(1)第一小组做了三次实验,至少两次实验成功的概率是
(2)第二小组在第4次成功前,共进行了6次试验,其中三次成功三次失败,且恰有两次连续失败,就是3次成功试验的间隔4空中选2个空,一个空位放置2次连续失败,一个放置一次失败,
其各种可能的情况种数为

因此所求的概率为
知识点
某产品按行业生产标准分成








3 5 3 3 8 5 5 6 3 4
6 3 4 7 5 3 4 8 5 3
8 3 4 3 4 4 7 5 6 7
该行业规定产品的等级系数


(1)试分别估计该厂生产的产品的一等品率、二等品率和三等品率;
(2)从样本的一等品中随机抽取2件,求所抽得2件产品等级系数都是8的概率。
正确答案
见解析
解析
解析:(1)由样本数据知,30件产品中,一等品有6件,二等品有9件,三等品有15件. …………3分
∴样本中一等品的频率为
故估计该厂生产的产品的一等品率为
二等品的频率为

三等品的频率为

(2)样本中一等品有6件,其中等级系数为7的有3件,等级系数为8的也有3件, ……………………7分
记等级系数为7的3件产品分别为


















记从“一等品中随机抽取2件,2件等级系数都是8”为事件
则

故所求的概率
知识点
在区间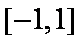
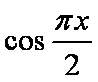
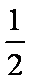
正确答案
解析
试题分析:本题是求几何概型概率,测度为长度.由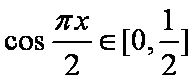
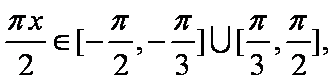
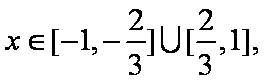
知识点
在长为




正确答案
解析
设




知识点
某初中校共有学生1200名,各年级男、女生人数如下表:
已知在全校学生中随机抽取l名,抽到七年级女生的概率是0.17。
(1)求a的值;
(2)现用分层抽样的方法在全校抽取200名学生,问应在九年级抽取多少名学生?
(3)已知175≤b≤183,求九年级中女生不少于男生的概率。
正确答案
见解析。
解析
(1)由题意,得a=1200×0.17=204;
(2)由(1)及已知条件,得
七年级共有学生:204+198=402(名)。
八年级共有学生:216+222=438(名)。
所以九年级共有学生:1200﹣402﹣438=360(名)。
所以应在九年级抽取学生数:360×
(3)由(2)可知九年级共有学生360名。
则九年级中女生人数及男生人数的所有可能结果为:
(175,185),(176,184),(177,183),(178,182),(179,181),(180,180),(181,179),(182,178),(183,177)共9中。
其中女生不少于男生的可能结果为:(180,180),(181,179),(182,178),(183,177)共4种。
所以九年级中女生不少于男生的概率为:P=
知识点
爸爸和亮亮用4张扑克牌(方块2,黑桃4,黑桃5,梅花5)玩游戏,他俩将扑克牌洗匀后,背面朝上放置在桌面上,爸爸先抽,亮亮后抽,抽出的牌不放回。
(1)若爸爸恰好抽到了黑桃4。
①请把右面这种情况的树形图绘制完整;
②求亮亮抽出的牌的牌面数字比4大的概率。
(2)爸爸、亮亮约定,若爸爸抽到的牌的牌面数字比亮亮的大,则爸爸胜;反之,则亮亮赢,你认为这个游戏是否公平?如果公平,请说明理由,如果不公平,更换一张扑克牌使游戏公平。
正确答案
(1) 
解析
(1)由于抽出的牌不放回,亮亮抽出的牌只能为方块2,黑桃5,梅花5这三种,因此树形图对应三种情况. 亮亮抽出的牌的牌面数字比4大的事件数就是统计结果中纵坐标数字大于4的结果数为2,因此所求概率为
列出所有情况的树形图:

统计出爸爸抽到的牌的牌面数字比亮亮的大,即有5种情况,因此爸爸胜的概率只有

试题解析:(1) ① 树形图:
②所以亮亮抽出的牌的牌面数字比4大的概率是
(2)不公平,理由如下:
爸爸抽出的牌的牌面数字比亮亮的大有5种情况,其余均为小于等于亮亮的牌面数字
所以爸爸胜的概率只有
只需把黑5改成3即可
知识点
扫码查看完整答案与解析