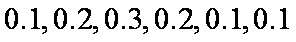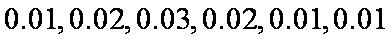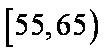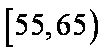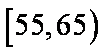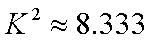- 随机事件及其概率
- 共412题
把正奇数依次按第一个括号1个数,第二个括号2个数,第三个括号3个数,第四个括号1
个数,……如此循环为(1),(3,5),(7,9,11),(13),(15,17),(19,21,23),……。则2015这个奇数在第 个括号内。
正确答案
504
解析
略
知识点
2013年12月21日上午10时,省会首次启动重污染天气Ⅱ级应急响应,正式实施机动车车尾号限行,当天某报社为了解公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
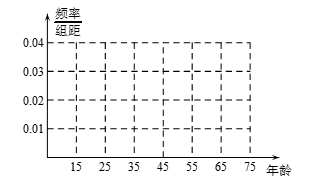
(1)完成被调查人员的频率分布直方图;
(2)若从年龄在[55,65),[65,75)的被调查者中各随机选取1人进行进行追踪调查,求两人中至少有一人赞成“车辆限行”的概率。
正确答案
见解析
解析
(1)各组的频率分别是
所以图中各组的纵坐标分别是
……………………5分
(2)设A表示事件:年龄在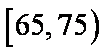
则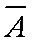
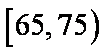
从年龄在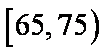
…………………7分
记年龄在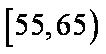
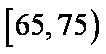
两人都不赞成“车辆限行”的所有可能结果为:ac,bc. ………………10分
知识点
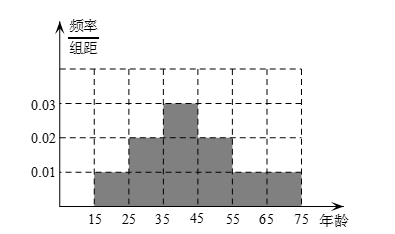
右图是依据某城市年龄在20岁到45岁的居民上网情 况调查而绘制的频率分布直方图,现已知年龄在 [30,35)、[35,40)、[40,45]的上网人数呈现递减的等差数列分布,则年龄在[35,40)的网民出现的频率为
正确答案
解析
由









知识点
近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重。大气污染可引起心悸、呼吸困难等心肺疾病。为了解某市心肺疾病是否与性别有关,在某医院随机的对入院50人进行了问卷调查得到了如下的列联表:
已知在全部50人中随机抽取1人,抽到患心肺疾病的人的概率为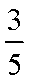
(1)请将上面的列联表补充完整;
(2)是否有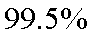
(3)已知在患心肺疾病的10位女性中,有3位又患胃病,现在从患心肺疾病的10位女性中,选出3名进行其他方面的排查,记选出患胃病的女性人数为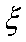
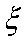
下面的临界值表供参考:
(参考公式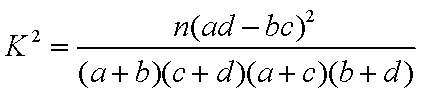
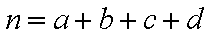
正确答案
见解析。
解析
(1):列联表补充如下 ………2分
(2):因为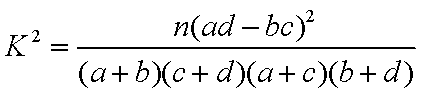
又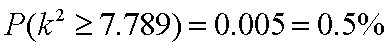
那么,我们有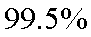
(3): 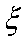
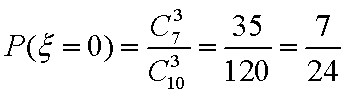
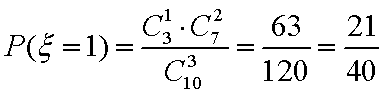
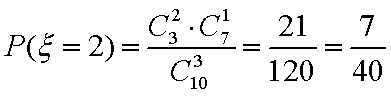
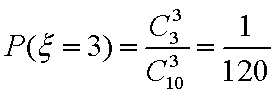
分布列如下: ………8分
则
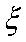
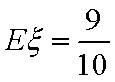
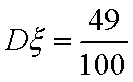
知识点
某商场为了了解顾客的购物信息,随机的在商场收集了100位顾客购物的相关数据,整理如下:
统计结果显示100位顾客中购物款不低于100元的顾客占60%,据统计该商场每日大约有5000名顾客,为了增加商场销售额度,对一次性购物不低于100元的顾客发放纪念品(每人一件)。(注:视频率为概率)
(1)试确定m,n的值,并估计该商场每日应准备纪念品的数量;
(2)为了迎接店庆,商场进行让利活动,一次购物款200元及以上的一次返利30元;一次性购物款小于200元的按购物款的百分比返利,具体见下表:
请估计该商场日均让利多少元?
正确答案
(1)m=20,n=20;3000(2)52000
解析
解析:(1)由已知,100位顾客中购物款不低于100元的顾客有


该商场每日应准备纪念品的数量大约为 
(2)设购物款为
当

当

当

当

所以估计日均让利为
…………10分

知识点
某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
(1)由表中数据直观分析,收看新闻节目的观众是否与年龄有关?
(2)用分层抽样的方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?
(3)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率。
正确答案
(1)有关(2)3名(3)
解析
(1)有关,收看新闻节目的观众多为年龄大的. ………………………………………3分
(2)应抽取的人数为:
(3)由(2)知,抽取的5名观众中,有2名观众的年龄处于20至40岁,
3名观众的年龄大于40岁. ………………………………………………………………8分
所求概率为:
知识点
某电视台举办青年歌手大奖赛,有10名评委打分,已知甲、乙两名选手演唱后的打分情况如茎叶图所示:
(1)从统计的角度,你认为甲与乙比较,演唱水平怎样?
(2)现场有3名点评嘉宾A、B、C,每位选手可以从中选2位进行指导,若选手选每位点评嘉宾的可能性相等,求甲乙两选手选择的点评嘉宾恰重复一人的概率。
正确答案
见解析。
解析
(1)由茎叶图可得:


所以甲演唱水平更高一点,但甲的方差较大,即评委对甲的水平认可存在较大的差异
(2)依题意,共有9个基本事件:
其中,甲乙两选手选择的点评嘉宾恰重复一人包含6个基本事件。
所以,所求概率为
知识点
2012年第三季度,国家电网决定对城镇居民民用电计费标准做出调整,并根据用电情况将居民分为三类: 第一类的用电区间在(0,170],第二类在(170,260],第三类在(260,+∞)(单位:千瓦时)。 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示。
(1) 求该小区居民用电量的中位数与平均数;
(2) 本月份该小区没有第三类的用电户出现,为鼓励居民节约用电,供电部门决定:对第一类每户奖励20元钱,第二类每户奖励5元钱,求每户居民获得奖励的平均值;
(3) 利用分层抽样的方法从该小区内选出5户居民代表,若从该5户居民代表中任选两户居民,求这两户居民用电资费属于不同类型的概率。
正确答案
(1)中位数:155,平均数:156.8(2)17元(3)
解析
(1) 因为在频率分布直方图上,中位数的两边面积相等,可得中位数为155. (2分)
平均数为 
(2)
(3)由题可知,利用分层抽样取出的5户居民中属于第一类的有4户,编为


















知识点
某城市持续性的雾霾天气严重威胁着人们的身体健康,汽车的尾气排放是造成雾霾天气的重要因素之一,为此该城市实施了机动车尾号限行政策。现有家报社想调查了解该市区公民对“车辆限行”的态度,并在该城市里随机抽查了50人,将调查情况进行整理后制成下表:
(1)请估计该市公民对“车辆限行”的支持率(答案用百分比表示);
(2)若从年龄在[15,25),[25,35)的被调查者中采用分层抽样选取3人进行跟踪调查,求选取的3人中有2人不支持“车辆限行”的概率。
正确答案
见解析
解析
解:(1)由表中可得支持率是
(2)在[15,25),[25,35)的被调查者中的六人编号:
把[15,25)中的两人编号:1号为不支持,2号为支持;
把[25,35)中的四人编号:3号为支持,4号为支持,5号为支持,6号为不支持。
利用分层抽样则应该在[15,25)、[25,35)分别抽取1人、2人,则所有可能如下:
(1,3,4),(1,3,5),(1,3,6),(1,4,5),(1,4,6),(1,5,6)
(2,3,4),(2,3,5),(2,3,6),(2,4,5),(2,4,6),(2,5,6)
以上共有12种情形,其中有2人不支持的有3种情形,
所以选取的3人中有2人不支持“车辆限行”的概率为
知识点
从2名男生和2名女生中,任意选择两人在星期六、星期日参加某公益活动,每天一人,则星期六安排一名男生、星期日安排一名女生的概率为( )
正确答案
解析
由题意知本题是一个古典概型,
试验包含的所有事件是从4个人安排两人,总共有C42A22=12种。
其中期六安排一名男生、星期日安排一名女生,总共有C21C21=4种,
∴其中至少有1名女生的概率P=
知识点
扫码查看完整答案与解析