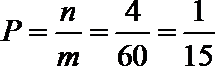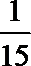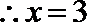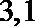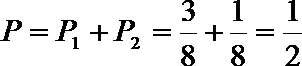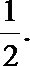- 随机事件及其概率
- 共412题
18.某中学的高二(1)班男同学有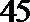
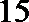
(Ⅰ)求某同学被抽到的概率及课外兴趣小组中男、女同学的人数;
(Ⅱ)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出
(Ⅲ)试验结束后,第一次做试验的同学得到的试验数据为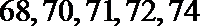
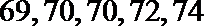
正确答案
解:(Ⅰ)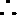
设有

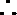
(Ⅱ)把
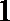
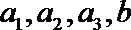
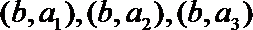

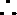
(Ⅲ)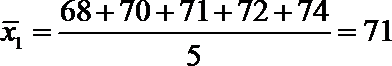
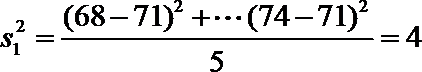
解析
解析已在路上飞奔,马上就到!
知识点
18. 实验中学的三名学生甲、乙、丙参加某大学的自主招生考核测试,在本次考核中只有合格和优秀两个等次,若考核为合格,则授予10分降分资格;考核为优秀,授予20分降分资格。假设甲、乙、丙考核为优秀的概率分别为


(1)求在这次考核中,甲、乙、丙三名同学中至少有一名考核为优秀的概率;
(2)记在这次考核中甲、乙、丙三名同学所得的降分之和为随机变量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知样本:
那么频率为0.2的范围是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.甲、乙两人下棋,两人下成和棋的概率是


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若以连续掷两次骰子分别得到的点数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.
(Ⅰ)上表是年龄的频率分布表,求正整数a,b的值;
(Ⅱ)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?
(Ⅲ)在(Ⅱ)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1人年龄在第3组的概率.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某商场准备在五一劳动节期间举行促销活动,根据市场调查,该商场决定从2种服装商品、3种家电商品、5种日用商品中,选出3种商品进行促销活动。
(I)试求选出的3种商品中至少有一种是日用商品的概率;
(II)商场对选出的A商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高120元,同时允许顾客有3 次抽奖的机会,若中奖,则每次中奖都可获得60元奖金,假设顾客每次抽奖时获奖与否是等可能的。试求某位顾客所中奖金数不低于商场提价数的概率。
正确答案
解:(I)从2种服装商品,3种家电商品,5种日用商品中,选出3种商品,一共有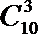

(II)要使所中奖金数不低于商场提价数,则该顾客应中奖两次或三次,分别得奖金120元和180元。
顾客每次抽奖时获奖与否是等可能的,其概率都是
所以中奖两次的概率是:
中奖三次的概率是
故中奖两次或三次的概率:
即所中奖金数不低于商场提价数的概率等于
说明:其他解法请酌情给分。
解析
解析已在路上飞奔,马上就到!
知识点
17.一汽车厂生产A,B,C三类轿车, 每类轿车均有舒适型和标准型两种型号, 某月的产量如表所示(单位:辆),若按A, B, C三类用分层抽样的方法在这个月生产的轿车中抽取50辆, 则A类轿车有10辆.
(Ⅰ)求z的值;
(Ⅱ)用随机抽样的方法从B类舒适型轿车中抽取8辆, 经检测它们的得分如下: 9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2. 把这8辆轿车的得分看作一个总体, 从中任取一个分数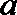
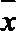

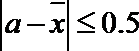

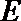
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.某校高三年级共有450名学生参加英语口语测试,其中男生250名,女生200名。现按性别用分层抽样的方法从中抽取45名学生的成绩。
(I)求抽取的男生与女生的人数?
(II)从男生和女生中抽查的结果分别如下表1和表2;
分别估计男生和女生的平均分数,并估计这450名学生的平均分数。(精确到0.01)
正确答案
解:(Ⅰ)由抽样方法知,被抽取的男生人数为250×=25,
被抽取的女生人数为200×=20.
(Ⅱ)男生甲和女生乙被抽到的概率均为0.1,
所以男生甲与女生乙至少有1人被抽到的概率:P=1-(1-0.1)2=0.19.
(Ⅲ)由(Ⅰ)知,m=25-(3+8+6)=8,n=20-(2+5+5)=8,
据此估计 男生平均分为=82.8,女生平均分为=83;
这450名学生的平均分数为≈82.33.
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析