- 随机事件及其概率
- 共412题
16.在一次百米比赛中,甲,乙等6名同学采用随机抽签的方式决定各自的跑道,跑道编号为1至6,每人一条跑道
(Ⅰ)求甲在1或2跑道且乙不在5或6跑道的概率;
(Ⅱ)求甲乙之间恰好间隔两人的概率.
正确答案
没有限制条件的种数为A66=720种,
(Ⅰ)先安排甲,再安排乙,剩下的全排,故有C21C31A44=144种,
根据概率公式,故甲在1或2跑道且乙不在5或6跑道的概率P=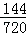
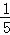
(Ⅱ)先选2人放在甲乙之间,并捆绑在一起,看作一个复合元素,再和剩下的2人全排,故有A42A22A33=144种,
根据概率公式,故甲乙之间恰好间隔两人的概率P=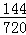
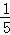
解析
解析已在路上飞奔,马上就到!
知识点
16.在一次百米比赛中,甲,乙等6名同学采用随机抽签的方式决定各自的跑道,跑道编号为1至6,每人一条跑道
(1)求甲在1或2 跑道且乙不在5或6跑道的概率 ;
(2)求甲乙之间恰好间隔两人的概率。
正确答案
(1)
(2)

)
解析
解析已在路上飞奔,马上就到!
知识点
13.从含有三件正品和一件次品的4件产品中不放回地任意取两件,则取出的两件中恰有一件次品的概率__________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.执行如图的程序框图,如果输入的n是4,则输出的p是___________
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
8.将3名学生安排到


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是:
(Ⅰ)求图中

(Ⅱ)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取5名参加中心广场的宣传活动,再从这5名中采用简单随机抽样方法选取3名志愿者担任主要负责人,求这3名志愿者中“年龄低于35岁”的人数大于1的概率。
正确答案
(I)∵小矩形的面积等于频率,
∴除
500名志愿者中,年龄在

(II)用分层抽样的方法,从中选取5名,则其中年龄“低于35岁”的人有3名,“年龄不低于35岁”的人有2名.
由列举法可得,总共为20种,
符合条件的为14种,概率为
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数
(1)从区间





(2)若连续掷两次骰子(骰子六个面上标注的点数分别为






正确答案
(1)




即

(2)由已知:
所以
即




当


当


当


满足

而基本事件总数为

解析
解析已在路上飞奔,马上就到!
知识点
11.已知某商
正确答案
1211
解析
解析已在路上飞奔,马上就到!
知识点
10.袋中装有同样大小的




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 为预防
已知在全体样本中随机抽取1个,抽到B组疫苗有效的概率是0.33.
(1)求
(2)现用分层抽样的方法在全体样本中抽取360个测试结果,问应在C组抽取多少个?
(3)已知
正确答案
(1)
即

(2)C组样本个数为y+z=2000-(673+77+660+90)=500,
现
(3)设测试不能通过事件为A ,C组疫苗有效与无效的可能的情况记为(y,z) 由(2)知 

(465,35)、(466,34)、(467,33)、……(475,25)共11个
若测试不能通过,则77+90+z>200,即z>33
事件A包含的基本事件有:((465,35)、(466,34)共2个


解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析


















