- 感生电动势、动生电动势
- 共108题
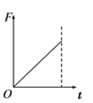
19.相距L=1 m的足够长金属导轨竖直放置,质量为m1=1 kg的金属棒ab和质量为m2=0.02 kg的金属棒cd均通过棒两端的套环水平地套在金属导轨上,如图所示,虚线上方磁场的磁感应强度B=1T,方向垂直纸

⑴当时间t=2s时拉力F的大小;
⑵当cd棒通过2C的电量时,其产生的热量为2.5J,则外力F需要做功为多少;
⑶判断cd棒将做怎样的运动,求出cd棒达到最大速度所需的时间t0,
正确答案
(1)F=11.5N
(2)WF=93J
(3)见解析
解析
⑴ 



⑵ 





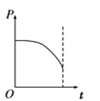
⑶ cd棒先做加速度逐渐减小的加速运动,当cd棒所受重力与滑动摩擦力相等时,速度达到最大;后做加速度逐渐增大的减速运动,最后停止运动.当cd棒速度达到最大时,有:


对abcd回路,有:

又
fcd随时间变化的图象如图所示。
考查方向
解题思路
(1)由E=BLv、 
(2)由



(3)分析cd棒的运动情况:cd棒先做加速度逐渐减小的加速运动,当cd棒所受重力与滑动摩擦力相等时,速度达到最大;然后做加速度逐渐增大的减速运动,最后停止运动.
cd棒达到最大速度时重力与摩擦力平衡,而cd棒对导轨的压力等于安培力,可求出电路中的电流,再由E=BLv、欧姆定律求出最大速度.
易错点
本题中cd棒先受到滑动摩擦,后受到静摩擦,发生了突变,要仔细耐心分析这个动态变化过程.滑动摩擦力与安培力有关,呈现线性增大.
知识点
如图所示,在竖直平面内有一质量为2m的光滑“


40.求整个过程中,克服安培力做的功。
41.求EF刚要出磁场Ⅰ时产生的感应电动势。
42.线框的EF边追上金属棒MN时,金属棒MN的动能?
正确答案
解析
整个过程中,只有线框EFCD受到的安培力做功。对线框EFCD,从静止到EF到达Ⅰ区域的下边界过程,根据动能定理,得到

考查方向
解题思路
首先根据动能定理可以求安培力做功,同过感应电动势公式求解电动势,再利用运动规律,动能定理求动能。
易错点
动能定理的计算以及金属棒在这个过程中的运功特点
正确答案
解析
对MN,细线刚好断裂前,


EF刚要出磁场Ⅰ时产生的感应电动势
考查方向
解题思路
首先根据动能定理可以求安培力做功,同过感应电动势公式求解电动势,再利用运动规律,动能定理求动能。
易错点
动能定理的计算以及金属棒在这个过程中的运功特点
正确答案
解析
设下落时间t时追上。
对MN,


追上时,MN的速度为
考查方向
解题思路
首先根据动能定理可以求安培力做功,同过感应电动势公式求解电动势,再利用运动规律,动能定理求动能。
易错点
动能定理的计算以及金属棒在这个过程中的运功特点
如图a所示,水平放置着两根相距为d=0.1 m的平行金属导轨MN与PQ,导轨的电阻忽略不计且两导轨用一根电阻也不计的导线相连.导轨上跨放着一根粗细均匀长为L=0.3m、电阻R=3.0 Ω的金属棒ab,金属棒与导轨正交,交点为c、d. 整个空间充满垂直于导轨向上的磁场,磁场B随时间变化的规律如图b所示. 开始时金属棒在3s前静止距离NQ为2m处,3s后在外力作用下以速度v=4.0 m/s向左做匀速直线运动,试求:
13.0~3S末回路中产生电流的大小和方向;
14.6 S ~8S过程中通过金属棒横截面的电荷量为多少?
15. t=12s时金属棒ab两端点间的电势差为多少?
正确答案
0.6A 顺时针;
解析
(1) 3S末回路中产生电流的方向为顺时针方向,由图b可知,3s末磁感应强度 B=1.5T
回路中产生的感生电动势为 E感=
回路中感应电流为:
考查方向
解题思路
首先根据法拉第电磁感应定律求出电动势,然后在计算电流和电势差
易错点
求电荷量不能用瞬时电流,电势差不等于电动势
正确答案
1.6C
解析
(2)E=BdV=0.8V

q=It=
考查方向
解题思路
首先根据法拉第电磁感应定律求出电动势,然后在计算电流和电势差
易错点
求电荷量不能用瞬时电流,电势差不等于电动势
正确答案
1.6V
解析
(3) t=12s时金属棒ab两端点间的电势差U=B(L-d)V=1.6V
考查方向
解题思路
首先根据法拉第电磁感应定律求出电动势,然后在计算电流和电势差
易错点
求电荷量不能用瞬时电流,电势差不等于电动势
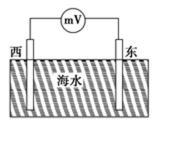
6. 北半球某处,地磁场水平分量B1=0.8×10-4T,竖直分量B2=0.5×10-4T,海水向北流动,海洋工作者测量海水的流速时,将两极板插入此海水中,保持两极板正对且垂线沿东西方向,两极板相距d=20m,如图所示,与两极板相连的电压表(可看做是理想电压表)示数为U=0.2mV,则
正确答案
解析
由题意知,海水向北流动,根据右手定则可知,西侧极板电势高,东侧极板电势低,A对B错;C、正负离子在两极板聚集,两极板间形成电场,最终最终正负离子受电场力和洛伦兹力处于平衡,由平衡条件得:qvB=q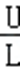
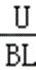
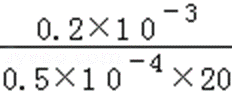
考查方向
解题思路
海水向南流动时,正负离子向南流动,受到洛伦兹力向东西方向偏转,打在两极板上,在两极板间形成电场,最终正负离子受电场力和洛伦兹力处于平衡,根据平衡求出流速
易错点
本题的关键知道海水向北流动时,正负离子向北流动,受到洛伦兹力向东西方向偏转,打在两极板上,在两极板间形成电场,最终正负离子受电场力和洛伦兹力处于平衡
知识点
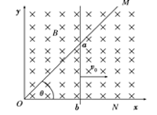
7. 如图所示,顶角θ=45°的金属导轨MON固定在水平面内,导轨处在方向竖直向下、磁感应强度为B的匀强磁场中.一根与ON垂直的导体棒在水平外力作用下以恒定速度v0沿导轨MON向右滑动,导体棒的质量为m,导轨与导体棒单位长度的电阻均为r.导体棒与导轨接触点为a和b,导体棒在滑动过程中始终保持与导轨良好接触.t=0时导体棒位于顶角O处,则流过导体棒的电流强度I、导体棒内产生的焦耳热Q、导体棒做匀速直线运动时水平外力F、导体棒的电功率P各量大小随时间变化的关系正确的是
正确答案
解析
A、0到t时间内,导体棒的位移为:x=v0t
t时刻,导体棒的长度为:l=x
导体棒的电动势为:E=Blv0
回路总电阻为:R=(2x+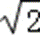
电流强度为: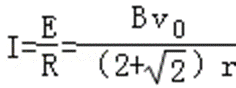
C、导体棒匀速直线运动,水平外力与安培力二平衡,则有: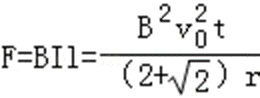
D、t时刻导体棒的电功率:P=I2R′=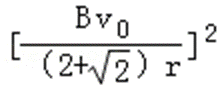
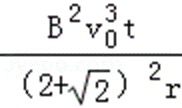
B、因为:P∝t
所以:Q=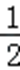
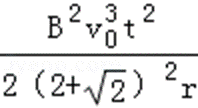
考查方向
解题思路
求出t时刻导体棒的有效长度,结合切割产生的感应电动势和闭合电路欧姆定律求出电流强度与时间的关系式.
导体棒在0~t时间内电流大小恒定,抓住R与时间正比,通过平均功率,根据Q=Pt求出产生的焦耳热Q.
导体棒做匀速直线运动时,水平外力等于安培力,根据平衡条件求出水平拉力的表达式
易错点
综合考查了切割产生的感应电动势、闭合电路欧姆定律、牛顿第二定律等知识点,综合性较强,关键得到感应电流不变
知识点
20.如右图所示,两固定的竖直光滑金属导轨足够长且电阻不计。两质量、长度均相同的导体棒c、d,置于边界水平的匀强磁场上方同一高度h处。磁场宽为3h,方向与导轨平面垂直。先由静止释放c,c刚进入磁场即匀速运动,此时再由静止释放d,两导体棒与导轨始终保持良好接触。用ac表示c的加速度,Ekd表示d的动能,xc、xd分别表示c、d相对释放点的位移。图中正确的是 ( )
正确答案
解析
A、B,设c、d刚进磁场时速度为v,c刚进入磁场做匀速运动,此时由静止释放d.设d经时间t进入磁场,并设这段时间内c的位移为x则
由于h=
d进入磁场后,cd二者都做匀速运动,且速度相同,二者与导轨组成的回路磁通量不变,感应电流为零,不受安培力,两导体棒均做加速度为g的匀加速运动,故A错误,B正确;
C、D,c出磁场时d下落2h,c出磁场后,只有导体棒d切割磁感线,此时d的速度大于进磁场时的速度,d受到安培力作用做减速运动,动能减小,d出磁场后动能随下 落高度的增加而均 匀增大,故C错误,D正确.
考查方向
解题思路
未进入磁场时,c、d做自由落体运动,到达磁场上边界时速度相同.c、d都进入磁场后,同时在磁场中运动时,两者速度相同,没有感应电流产生,只受重力,都做匀加速直线运动,加速度为g.c出磁场后,d在切割磁感线时,此时d的速度比进磁场时大,产生感应电动势增大,感应电流增大,受到的安培力增大,则d做匀减速直线运动.根据动能与高度的关系选择动能图象.
易错点
关键在于分析两导体的受力情况和运动情况,抓住安培力大小与速度大小成正比这个结论,分析只有d切割磁感线过程d的运动情况
知识点
2.图甲为水平放置的两根平行光滑导轨,处在垂直轨道平面向里的匀强磁场中。均匀金属棒AB垂直于导轨水平静止放置。从t=0时刻开始在AB棒上通有图乙所示的交变电流,规定甲图所示的电流方向为正方向。下列说法正确的是( )
正确答案
解析
根据左手定则可知,当电流的方向向下时,棒受到的安培力的方向向右;同理,当电流的方向向上上,则棒受到的安培力的方向向左.
A、由于电流随时间按照正弦规律变化,而安培力:F=BIL与电流成正比,所以导体棒受到的安培力也随时间按照正弦规律变化,在前半个周期内(0﹣t2时间内)棒受到的安培力的方向向右,所以棒向右做加速运动;在后半个周期内棒受到的安培力的方向向左,将向右做减速运动,由于加速阶段的加速度和减速阶段的加速度具有对称性,所以由运动的对称性可知,当t=t4时刻棒的速度恰好为0;而后,在以后的歌周期内棒将不断重复第一个周期内的运动.所以棒将一直向右运动.故A错误;
B、导体棒在前半个周期内(0﹣t2时间内)棒受到的安培力的方向向右,所以棒向右做加速运动,后半个周期内棒受到的安培力的方向向左,将向右做减速运动,所以t2时刻导体棒的速度最大.故B错误;
C、由于安培力:F=BIL与电流成正比,所以导体棒受到的安培力也随时间按照正弦规律变化,在t1时刻导体棒受到的安培力最大,所以加速度最大.故C错误;
D、导体棒一直向右运动,前半个周期内(0﹣t2时间内)棒受到的安培力的方向向右,安培力做正功;后半个周期内棒受到的安培力的方向向左,安培力做负功.故D正确.
故选:D
考查方向
解题思路
根据F=BIL分析安培力随电流的变化关系,由牛顿第二定律分析导体棒的加速度的变化,结合运动的对称性分析导体棒运动的规律即可.
易错点
该题结合安培力随电流变化的规律,考查牛顿第二定律的瞬时性的理解与应用能力,解答该题,关键要从运动的对称性来考虑,明确在t=t4时刻导体棒的速度为0.
知识点
15.如图,直角三角形金属框abc放置在匀强磁场中,磁感应强度大小为B,方向平行于ab边向上。当金属框绕ab边以角速度
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析