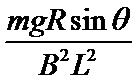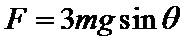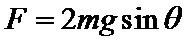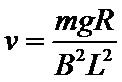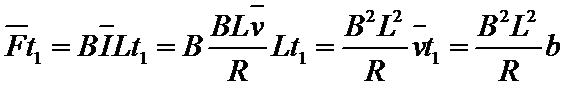- 感生电动势、动生电动势
- 共108题
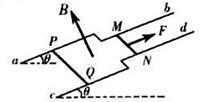
8．如图所示，光滑金属导轨ab和cd构成的平面与水平面成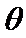
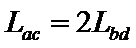
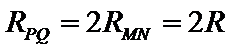
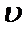
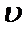
AMN中电流方向是由M到N
B匀速运动的速度
C在MN、PQ都匀速运动的过程中，
D在MN、PQ都匀速运动的过程中，
正确答案
解析
A.根据右手定则可知，MN中电流方向是由M到N，故A正确；
B.由题意可知回路中的电流为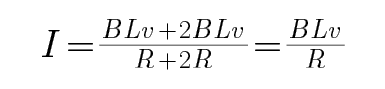
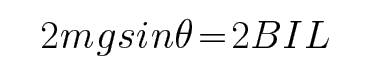
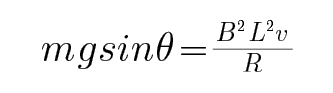
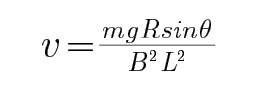
CD.对MN根据平衡条件有：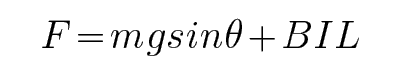
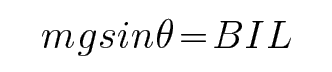
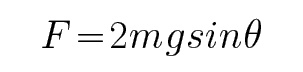
考查方向
法拉第电磁感应定律；右手定则；通电直导线在磁场中受到的力——安培力
解题思路
两导体棒在磁场中切割磁感线产生感应电动势，由右手定则判断电流方向，根据两棒的状态分析受力，根据平衡条件列出方程求解.
易错点
两个棒都切割磁感线产生感应电动势，关键会计算电路中的总电动势的大小.
知识点
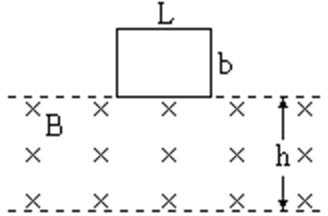
15.如图所示，在空中有一水平方向的匀强磁场区域，区域的上下边缘间距为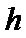
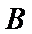
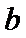
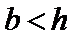
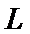
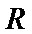
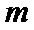
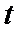
正确答案
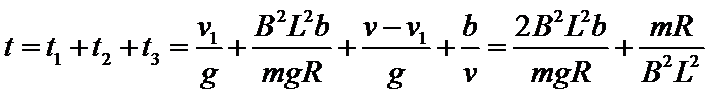
解析
设线圈匀速穿出磁场区域的速度为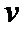
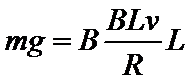
对线圈从开始到刚好完全进入磁场的过程，经历的时间设为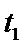
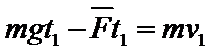
解得：
因为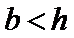
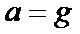
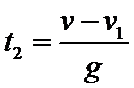
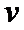
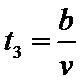
故
考查方向
感生电动势、动生电动势；动量定理；匀变速直线运动规律的综合运用
解题思路
线圈穿越磁场区域经历了三段过程：进入磁场、完全在磁场里面和穿出磁场，分段求时间的表达式．
易错点
关键分析清楚物体的运动过程，在线圈从开始到刚好完全进入磁场的过程，线圈受到重力和安培力，运用动量定理列式，得到时间表达式；线圈完全在磁场里运动过程，做匀加速运动，由运动学公式得到时间表达式；匀速穿出磁场过程，由运动学公式得到时间表达式．联立即可求得总时间．
知识点
电阻不计的平行金属导轨相距L，与总电阻为2R的滑动变阻器、板间距为d的平行板电容器和开关S连成如图所示的电路。磁感应强度为B的匀强磁场垂直导轨所在的平面。电阻为R的金属棒ab与导轨垂直，接触良好，并紧贴导轨匀速移动。合上开关S，当滑动变阻器触头P在中点时，质量为m、电量为+q的带电微粒从平行板电容器中间位置水平射入，微粒在两板间做匀速直线运动；当P移至C时，相同的带电微粒以相同的速度从同一位置射入两板间，微粒穿过两板的过程中动能增加
26.ab运动的方向及其速度大小；
27.当P移至C时，微粒穿过两板的过程中，电场力对微粒做的功W。
正确答案
解析
微粒做匀速直线运动时，电场力与重力平衡，则电场力方向竖直向上，上极板带负电，ab中感应电流方向由a与b，由右手定则判断知ab向左运动．对微粒，由平衡条件有：
得电容器板间电压为：
由
考查方向
导体切割磁感线时的感应电动势；带电粒子在匀强电场中的运动
解题思路
微粒做匀速直线运动时，电场力与重力平衡，分析电容器板间电场方向，确定金属棒产生的感应电流方向，由右手定则判断其运动方向．由平衡条件求电容器板间电压，得到金属棒产生的感应电动势，再由E=BLv求金属棒的速度.
易错点
关键分析带电粒子在匀强电场中的受力情况，由带电粒子做直线运动的条件求解.
正确答案
解析
当P移至C时，板间电压为：
微粒穿过两板的过程中，由动能定理得：
（qE电-mg）h=△Ek．
又
得：
故电场力对微粒做的功为：W=qE电h=4△Ek
考查方向
带电粒子在匀强电场中的运动
解题思路
当P移至C时，由电路知识求出电容器板间电压．此时微粒在电场中做类平抛运动，由动能定理求出偏转距离，再求电场力做功.
易错点
粒子在电场中做类平抛，关键应用动能定理列式求解.
如图，一对表面粗糙的平行金属轨道竖直固定在水平地面上，轨道与地面绝缘，轨道顶端连接有一定值电阻R，在A1A2、A3A4区域内有垂直于轨道平面向里的匀强磁场．一水平金属杆CD通过两金属环套在轨道上，现使金属杆CD以某一初速度竖直向上运动，穿过磁场区域后继续上升到最高位置A5A6，然后落回地面，此后不再运动．已知金属杆CD与轨道间的摩擦力大小恒为其重力的
求：
29.金属杆CD向上、向下两次经过A3A4位置时的速度之比；
30.金属杆CD向上运动经过A1A2刚进入磁场时的加速度大小；
31.金属杆CD向上、向下两次经过磁场区域的过程中定值电阻R上产生的焦耳热之比．
正确答案
解析
（1）设杆的质量为m，A3A4与A5A6间的距离为h，上升过程中的加速度大小为：
又
则
下降过程中的加速度大小为：
又
则
即：
考查方向
电磁感应中的力学
解题思路
对金属杆受力分析，由牛顿第二定理求出加速度，然后由运动学公式计算出速度v，即可求出比值。
易错点
金属杆CD向上、向下两次经过A3A4位置时没有安培力。
正确答案
解析
设杆的长度为
回路中的电流
杆受到的安培力大小
杆向上经过A1A2刚进入磁场时，由牛顿第二定理得：
得
由题意知，杆下落进人磁场做匀速直线运动的速度v2,
切割产生的电动势为：
回路中的电流为：
杆受到的安培力：
这一过程杆受力平衡：
可得：
代入数据得：
考查方向
电磁感应中的力学
解题思路
对金属杆CD向上运动经过A1A2刚进入磁场时受力分析，结合欧姆定律和牛顿第二定理就可求出加速度a。
易错点
此题过程复杂，运动状态复杂，要仔细分析清楚各不同阶段的运动情况和受力情况。
正确答案
解析
设A3A2与A3A4的距离为d，杆向上穿过磁场的过程中，由动能定理
杆下落 过程中，
由功能关系得：
即
考查方向
电磁感应中的能量
解题思路
根据功能关系，定值电阻R上产生的焦耳热数值上等于安培力做的功。
易错点
不会应用常见的功能关系。
2.平行导轨固定在水平桌面上，左侧接有阻值为R的电阻，导体棒ab与导轨垂直且接触良好，ab棒在导轨间的阻值为r。输出功率恒为P的电动机通过水平绳向右拉动ab棒。整个区域存在竖直向上的匀强磁场。若导轨足够长，且不计其电阻和摩擦。则电阻R消耗的最大功率为（）
AP
B
C
D
正确答案
解析
当导体棒ab做匀速运动时，电阻R消耗的功率最大，此时电动机做功全部转化为电能，电能又全部转化为电路中的焦耳热，因此电路的功率等于电动机的输出功率P，根据闭合电路欧姆定律及串并联电路的关系可知电阻R消耗的最大功率为
考查方向
电功、电功率；焦耳定律；串联电路和并联电路
解题思路
根据题意可知，导体棒在移动过程中要切割磁感线，产生感应电动势，与电阻R组成回路，导体棒又受到安培力的作用，当导体棒ab做匀速运动时，电阻R消耗的功率最大，根据能量转化关系可知此时电路消耗的功率等于电动机的输出功率P，再根据串并联的关系得出R此时消耗的功率.
易错点
分析出导体棒ab匀速运动时，电阻R消耗的功率最大是解题的关键.
知识点
扫码查看完整答案与解析