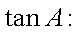- 任意角的概念
- 共394题
1
题型:简答题
|
在△ABC中,角A,B,C所对的边分别为a,b,c,且
(1)求B;
(2)若
正确答案
见解析。
解析
(1)由

所以


因为在△ABC中,sinA≠0,sinC≠0,
所以cosB=
因为B(0,π),所以
(2)因为

因为

所以
=
知识点
任意角的概念
1
题型:填空题
|
在△ABC中,若9cos2A﹣4cos2B=5,则
正确答案

解析
在△ABC中,∵9cos2A﹣4cos2B=5,∴9(1﹣2sin2A )﹣4(1﹣2sin2B)=5,
化简可得 9sin2A=4sin2B,故有 

由正弦定理可得 


故答案为 
知识点
任意角的概念
1
题型:
单选题
|
如图,正五边形





正确答案
C
解析
因为














知识点
任意角的概念
1
题型:填空题
|
如图,在等腰三角形ABC中,底边BC=2,





正确答案
0
解析
∵在等腰三角形ABC中,底边BC=2,∴可取BC的中点O作为坐标原点距离平面直角坐标系。
则B(﹣1,0),C(1,0),
设A(0,a)(a>0),∵

∴


∵



∴
∵




∴
∴


故答案为0。
知识点
任意角的概念
1
题型:填空题
|
在△ABC中,若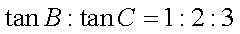
正确答案
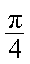
解析
设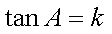
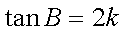
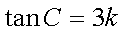
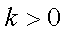
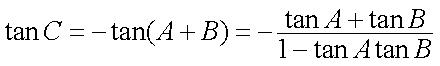
求得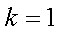
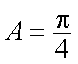
知识点
任意角的概念
下一知识点 : 终边相同的角
扫码查看完整答案与解析