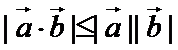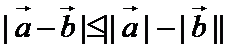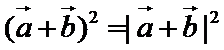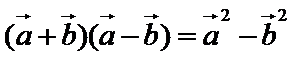- 平面向量的数量积及其应用
- 共555题
13.设向量a=(x,x+1),b=(1,2),且a 
正确答案

知识点
8.对任意向量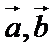
正确答案
解析
因为
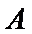
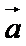
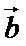
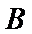
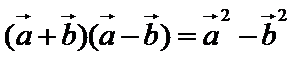
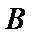
考查方向
解题思路
解题时一定要抓住重要字眼“不”,否则很容易出现错误.解本题需要掌握的知识点是向量的模和向量的数量积,即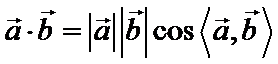
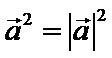
易错点
注意数量积定义
知识点
11.已知向量


正确答案
解析
由题意可知,


考查方向
解题思路
直接利用垂直数量积为0来计算。
易错点
粗心计算失误。
知识点
5.已知
正确答案
解析
由三角形的三遍关系和向量的集合意义得到


考查方向
平面向量 数量积的运算
解题思路
根据平面向量数量积的定义与运算性质,对每个选项判断即可
易错点
对平面向量的数量积的性质掌握不牢固
知识点
已知

(1)若

(2)设


正确答案
见解析。
解析
(1)∵
又∵




(2)∵








知识点
在




正确答案
解析
略
知识点
已知向量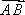
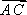
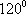
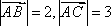

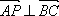
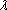
正确答案
解析
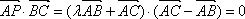
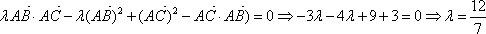
知识点
已知向量



(1)求函数


(2)在






正确答案
见解析。
解析
(1)由题意得:
所以
因为
所以当

函数


(2)由
又因为


由题意知 
所以
则
故所求边


知识点
已知平面向量




正确答案
解析
略
知识点
已知平面向量

正确答案
解析
略
知识点
扫码查看完整答案与解析