- 交集及其运算
- 共152题
1.已知集合A=[0，4]，B=[-2，3]，则A∩B=（ ）
正确答案
解析
在数轴上表示出来，就可以很清楚地知道结果A∩B=[0，3]，选B.
知识点
2.设A,B均为非空集合，且A∩B=⌀,A∪B={1,2,3,4}，记A,B中元素的个数分别为a,b,所有满足“a∈B，且b∈A”的集合对(A,B)的种类为（ ）
正确答案
解析
由A∪B={1,2,3,4},且A∩B=⌀,若a=1,b=3,则1∈B,3∈A,共1种；若a=2,b=2,则2∈B,2∈A,这与A∩B=⌀矛盾;若a=3,b=1,则3∈B,1∈A，共1种，所以共2种。
知识点
7.设[x]表示不大于x的最大整数，集合A={x|x2－2[x]=3}，B={x|
正确答案
解析
不等式
若x∈A∩B，则
若[x]≤-2，则x2=3+2[x]<0，没有实数解；
若[x]=-1，则x2=1，解得x=-1；
若[x]=0，则x2=3，没有符合条件的解；
若[x]=1，则x2=5，没有符合条件的解；
若[x]=2，则x2=7，有一个符合条件的解x=
因此A∩B=
知识点
1．已知全集U=R，集合A=｛x｜
A（0，1）
B（1，＋
C（一4，1）
D（一
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
1.已知全集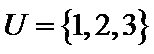
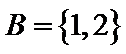
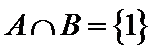
正确答案
解析
因为A中必含有元素1，不含元素2，可能含有元素3，所以共有2个满足题意的集合。
考查方向
解题思路
利用交集只有1这一个元素，然后集合A中必然含有元素1，不能含有元素2，然后分别举出所有的情况。
易错点
容易漏掉集合A里面的元素或者考虑问题的时候比较片面，出现集合A里面多出一个元素2。
知识点
2．已知集合A={x|y=
正确答案
解析
由
考查方向
解题思路
利用定义域所满足的条件得出集合A中X所满足的关系，解不等式得到集合B中y所满足的关系，然后求两个集合的交集．
易错点
1、本题易在解不等式上出错，搞不清集合的交并补运算 。
2、本题易搞不清楚是求定义域还是值域。
知识点
1．若集合
A
B
C
D
正确答案
解析
考查方向
解题思路
先解出一元二次不等式的解集，然后对两个集合取交集即可得
易错点
一元二次不等式解错
知识点
1．已知集合A={1，2}，B={1，m，3}，如果A∩B=A，那么实数m等于（ ）
正确答案
解析
由A∩B=A知
考查方向
解题思路
由A∩B=A知
易错点
对A∩B=A等价于
知识点
1. 已知全集
A
B
C
D
正确答案
解析
集合A中的代表元素为x,x的取值范围为
考查方向
解题思路
理解集合A和集合B中元素的特点
易错点
集合中元素的特征，集合A表示的意义
知识点
1．已知集合
A
B
C
D
正确答案
解析
因为
所以
应选B
考查方向
解题思路
化简集合A；
根据交集的定义直接得出答案，应选B
易错点
集合A中不等式的解法易出现错误；
集合的交集和并集概念混淆。
知识点
扫码查看完整答案与解析