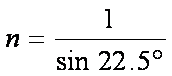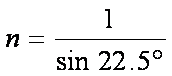全反射_章节学习

1

题型：填空题

|

填空题 · 9 分

一玻璃立方体中心有一点状光源。今在立方体的部分表面镀上不透明薄膜，以致从光源发出的光线只经过一次折射不能透出立方体。已知该玻璃的折射率为，求镀膜的面积与立方体表面积之比的最小值。

正确答案

解析

如图，考虑从玻璃立方体中心O点发出的一条光线，假设它斜射到玻璃立方体上表面发生折射。根据折射定律有

①

式中，n是玻璃的折射率，入射角等于θ，α是折射角。

现假设A点是上表面面积最小的不透明薄膜边缘上的一点。由题意，在A点刚好发生全发射，故

②

设光线OA在立方体上表面的投影长为RA，由几何关系有

③

式中a为玻璃立方体的边长。由①②③式得

④

由题给数据得

⑤

由题意，上表面所镀的面积最小的不透明薄膜应是半径为RA的圆。所求的镀膜面积与玻璃立方体的表面积S之比为

⑥

由⑤⑥式得

⑦

知识点

全反射

1

题型：单选题

|

单选题 · 6 分

在一次讨论中，老师问道：“假如水中相同深度处有a、b、c三种不同颜色的单色点光源，有人在水面上方同等条件下观测发现，b在水下的像最深，c照亮水面的面积比a的大，关于这三种光在水中的性质，同学们能做出什么判断？”有同学回答如下：

①c光的频率最大　　②a光的传播速度最小

③b光的折射率最大　④a光的波长比b光的短

根据老师的的假定，以上回答正确的是

A①②

B①③

C②④

D③④

正确答案

C

解析

由视深h′＝，知b光的折射率最小，由c光照亮的面积比a的大，知临界角Cc＞Ca，由sinC＝，得折射率na＞nc，则三种色光的折射率关系为na＞nc＞nb，③错，故选项B、D错误；由na＞nc＞nb知三种色光的频率为νa＞νc＞νb，①错，故选项A错误，则选项C正确。

知识点

光的反和折射全反射

1

题型：单选题

|

单选题 · 6 分

如图听示，口径较大、充满水的薄壁圆柱形玻璃缸底有一发光小球，则：（）

A小球必须位于缸底中心才能从侧面看到小球

B小球所发的光能从水面任何区域射出

C小球所发的光频率变大

D小球所发的光从水中进入空气后传播速度变大

正确答案

D

解析

略

知识点

光的反和折射全反射

1

题型：简答题

|

简答题 · 12 分

（1）如题图所示的装置,弹簧振子的固有频率是4 Hz. 现匀速转动把手,给弹簧振子以周期性的驱动力,测得弹簧振子振动达到稳定时的频率为1Hz,则把手转动的频率为 .

A.1 Hz

B.3 Hz

C.4 Hz

D.5 Hz

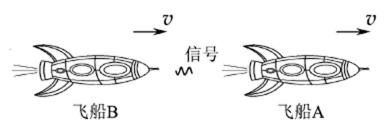
（2）如题图所示,两艘飞船A、B 沿同一直线同向飞行,相对地面的速度均为v(v 接近光速c). 地面上测得它们相距为L,则A 测得两飞船间的距离 (选填“大于”、“等于”或“小于”)L. 当B 向A 发出一光信号,A 测得该信号的速度为 .

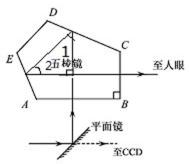
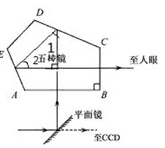
（3）题图为单反照相机取景器的示意图, ABCDE为五棱镜的一个截面,AB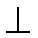BC. 光线垂直AB 射入,分别在CD 和EA 上发生反射,且两次反射的入射角相等,最后光线垂直BC 射出.若两次反射都为全反射,则该五棱镜折射率的最小值是多少?(计算结果可用三角函数表示)

正确答案

（1）A

（2）大于 c (或光速)

（3）

解析

（1）物体受迫振动的频率等于驱动力的频率，故选A。

（2）根据狭义相对论，两飞船接近光速，则距离应变大，而光速是不变的。

（3）

如图∠1=∠2=450，则可知入射角α=22.5o,则折射率最小值

知识点

外力作用下的振动全反射

1

题型：简答题

|

简答题 · 12 分

（1）激光具有相干性好，平行度好、亮度高等特点，在科学技术和日常生活中应用广泛，下面关于激光的叙述正确的是。

a激光是纵波

b频率相同的激光在不同介质中的波长相同

c两束频率不同的激光能产生干涉现象

d利用激光平行度好的特点可以测量月球到地球的距离

（2）如图甲所示，在杨氏双缝干涉实验中，激光的波长为5.30×m，屏上P点距双缝和的路程差为7.95×m，则在这里出现的应是（选填“明条纹”或“暗条纹”），现改用波长为6.30×m的激光进行上述实验，保持其他条件不变，则屏上的条纹间距将（选填“变宽”、“变窄”或“不变”）。

（3）如图乙所示，一束激光从O点由空气射入厚度均匀的介质，经下表面反射后，从上面的A点射出，已知入射角为i，A与O 相距l，介质的折射率为n，试求介质的厚度d。

正确答案

（1）d；

（2）暗条纹；变宽。

(3)

解析

（1）激光是电磁波，为横波，A错；频率相同的激光在不同介质中的波长是不同的，B错；能产生干涉的条件是两列光的频率相同，C错；测定距离就是利用激光的平行度高的特性，D正确。

（2），波程差是半波长的奇数倍，是暗条纹。

，变大，变大，变宽。

（3）设折射角为r，折射定律；几何关系

解得

知识点

光的反和折射全反射用双缝干涉实验测定光的波长激光的特性和应用

1

题型：简答题

|

简答题 · 15 分

（1）运动周期为T，振幅为A，位于x=0点的被波源从平衡位置沿y轴正向开始做简谐运动，该波源产生的一维简谐横波沿x轴正向传播，波速为，传播过程中无能量损失，一段时间后，该振动传播至某质点p，关于质点p振动的说法正确的是______。

A．振幅一定为A

B．周期一定为T

C．速度的最大值一定为v

D．开始振动的方向沿y轴向上或向下取决于它离波源的距离

E．若P点与波源距离s=vT，则质点P的位移与波源的相同

（2）一半圆柱形透明物体横截面如图所示，地面AOB镀银，o表示半圆截面的圆心，一束光线在横截面内从M点入射，经过AB面反射后从N点射出。已知光线在M点的入射角为30， MOA=60，NOB=30。求：

1）光线在M点的折射角

2）透明物体的折射率

正确答案

解析

（1）由波的形成与传播可知，正确答案是ABE。（选对一个给3分，选对两个给4分，选对三个给6分。每选错一个扣3分，最低得分为0分）

（2）1）解：如图，透明物体内部的光路为折线MPN，Q、M点相对于氏面EF对称，Q、P和N

三点共线。

设在M点处，光的和射角为i，折射角为r，

。根据题意有

①

由几何关系得，，于是

②

且③

由①②③式得④

2）解：根据折射率公式有

⑤

由④⑤式得 ⑥

知识点

简谐运动的描述光的反和折射全反射

1

题型：单选题

|

单选题 · 6 分

如题20图所示，空气中有一折射率为的玻璃柱体，其横截而是圆心角为90o,、半径为R的扇形OAB、一束平行光平行于横截面，以45o入射角射到OA上，OB不透光，若考虑首次入射到圆弧上的光，则上有光透出的部分的弧长为

A

B‍

C ‍

D‍‍‍

正确答案

B

解析

根据折射定律，可得光进入玻璃后光线与竖直方向的夹角为30°。过O的光线垂直入射到AB界面上点C射出，C到B之间没有光线射出；越接近A的光线入射到AB界面上时的入射角越大，发生全反射的可能性越大，根据临界角公式得临界角为45°，如果AB界面上的临界点为D，此光线在AO界面上点E入射，在三角形ODE中可求得OD与水平方向的夹角为180°-（120°+45°）=15°，所以A到D之间没有光线射出。由此可得没有光线射出的圆弧对应圆心角为90°-（30°+15°）=45°，为。

知识点

光的反和折射全反射

1

题型：简答题

|

简答题 · 4 分

如图所示，一段横截面为正方形的玻璃棒，中间部分弯成四分之一圆弧形状，一细束单色光由MN端面的中点垂直射入，恰好能在弧面EF上发生全反射，然后垂直PQ端面射出。

①求该玻璃棒的折射率。

②若将入射光向N端平移，当第一次射到弧面EF上时_____（填“能”“不能”或“无法确定能否”）发生全反射。

正确答案

① ；②能

解析

①发生全反射的临界角

C =arc sin

求得：n =

②由于入射角不变，在弧面EF上仍发生全反射。

知识点

全反射

1

题型：单选题

|

单选题 · 6 分

如图，一束光由空气射向半圆柱体玻璃砖，O点为该玻璃砖截面的圆心，下图能正确描述其光路图的是（）

A

B

C

D

正确答案

A

解析

略

知识点

光的反和折射全反射

1

题型：单选题

|

单选题 · 6 分

如图，半圆形玻璃砖置于光屏PQ的左下方。一束白光沿半径方向从A点射入玻璃砖，在O点发生反射和折射，折射光在光屏上呈现七色光带。若入射点由A向B缓慢移动，并保持白光沿半径方向入射到O点，观察到各色光在光屏上陆续消失。在光带未完全消失之前，反射光的强度变化以及光屏上最先消失的光分别是

A减弱，紫光

B减弱，红光

C增强，紫光

D增强,红光

正确答案

C

解析

同一介质对各色光的折射率不同，各色光对应的全反射的临界角也不同。七色光中紫光折射率最大，由n＝可知紫光的临界角最小，所以入射点由A向B缓慢移动的过程中，最先发生全反射的是紫光，折射光减弱，反射增强，故C正确。

知识点

光的反和折射全反射

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点