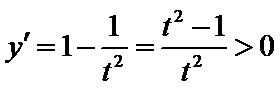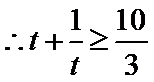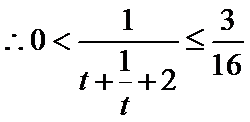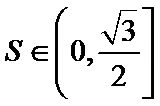- 椭圆的相关应用
- 共44题
如图,在平面直角坐标系





24.若


25.若直线


正确答案
(1)
解析
(1)由圆









联立①②,解得


考查方向
解题思路
先根据题中条件求出圆心的坐标,后即可得到圆
易错点
不知题中给出的直线
正确答案
(2)
解析
(2)因为直线








即

考查方向
解题思路
根据直线和圆相切得


易错点
不会化简


20.已知中心在原点,焦点在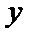
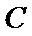
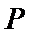
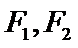
(1)求椭圆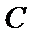
(2)若直线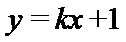
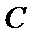
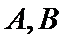
正确答案
(1)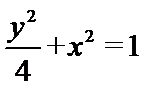
解析
试题分析:本题属于直线和椭圆位置关系的基本问题,题目的难度是逐渐由易到难,
(1)根据已知条件构造方程组;
(2)用设而不求的方法将面积表示成关于斜率的表达式,然后换元求出面积的取值范围。
(1)设椭圆的标准方程为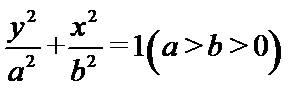
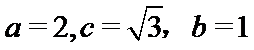
所以椭圆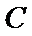
(2)设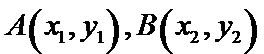
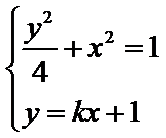
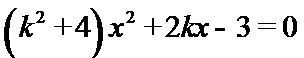
故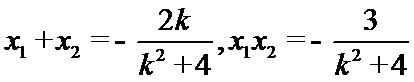
设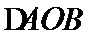

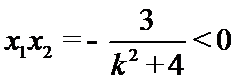
令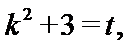
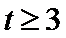
对函数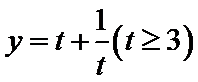
因此函数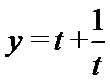
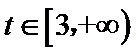
因此,
考查方向
解题思路
本题考查直线和椭圆的位置关系,解题步骤如下:
(1)根据已知条件构造方程组;
(2)用设而不求的方法将面积表示成关于斜率的表达式,然后换元求出面积的取值范围。
易错点
第二问不会用设而不求的方法来解决。
知识点
20. 如图,已知椭圆







(Ⅰ)若过点

(Ⅱ)在(Ⅰ)的条件下,若直线


正确答案
(1)

解析
试题分析:本题属于直线与圆锥曲线的问题,
(1)由已知条件构造方程组求解(2)用设而不求的方法来解决.
(Ⅰ)因为离心率





即
因为直线与原点的距离为
所以


(Ⅱ)解:因为直线











考查方向
解题思路
本题考查直线与圆锥曲线的问题,解题步骤如下:
由已知条件构造方程组求解。
用设而不求的方法来解决。
易错点
不会利用设而不求的思想来解答。
知识点
已知圆



23.求椭圆
24.椭圆






正确答案
详见解析
解析
(Ⅰ) 圆
圆心坐标为
过椭圆










考查方向
直线与圆的方程,求椭圆的标准方程
解题思路
先求出直线L的方程,然后求出a b c进而求出椭圆的标准方程
易错点
计算能力弱,相关公式定理混淆
正确答案
详见解析
解析
(Ⅱ)由(Ⅰ)知


由




考查方向
直线与圆锥曲线的结合题,直线的斜率
椭圆的几何性质
解题思路
设出相关参数,根据所给条件,建立方程,最后求出答案
易错点
计算能力弱,找不到恰当的等量关系
扫码查看完整答案与解析