- 利用导数证明不等式
- 共265题
在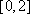
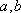
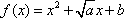
正确答案
解析
略
知识点
已知


(1)若曲线




(2)设




正确答案
(1)
(2)
解析
(1)



依题意有
可得


(2)
不妨设
则

即
设
则对任意的


等价于


可得
依题意有,对任意

由

知识点
已知f(x)=xlnx,
(1)当a=2时,求函数y=g(x)在[0,3]上的值域;
(2)求函数f(x)在[t,t+2](t>0)上的最小值;
(3)证明:对一切x∈(0,+∞),都有
正确答案
见解析。
解析
(1)
当x=1时,gmin(x)=g(1)=
故g(x)值域为
(2) f'(x)=lnx+l,当

①
②

③

所以
(3)g'(x)+1=x,所以问题等价于证明


设



知识点
已知函数

(1)若不等式

(2)求证:
正确答案
见解析。
解析
(1) 由

令







当



当





所以, (i)当

(ii)当

(iii)当
(2) 由(1)知 

∴
∴
∴
∵
∴ 
知识点
已知
则
正确答案
解析
=
又
令
令
所以,原式=
知识点
扫码查看完整答案与解析
































