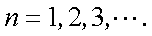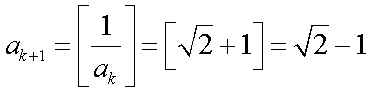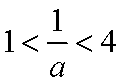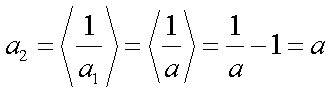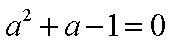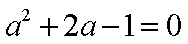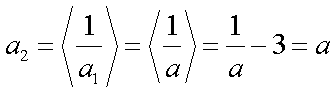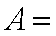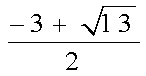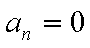- 利用导数证明不等式
- 共265题
已知数列

(1)试判断数列
(2)令
正确答案
见解析。
解析
(1)



(2)
∴原不等式成立. ………………………….12分
知识点
已知

(1)求数列
(2)等比数列




正确答案
见解析。
解析
(1)设等差数列
由

由

由①得

∴


∴
(2)
∴

错位相减可得:
整理得:

∴
知识点
对于实数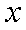
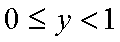
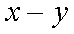
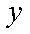
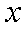
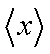
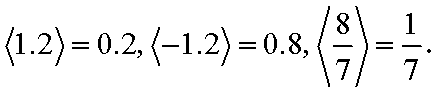
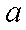
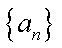
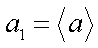
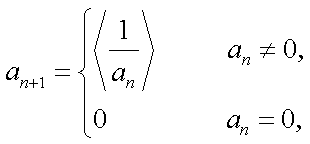
(1)若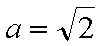
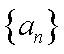
(2)当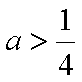
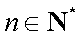
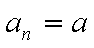

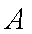
(3)若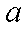
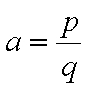
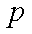
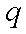
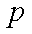
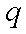
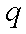
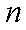
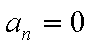
正确答案
见解析。
解析
(1)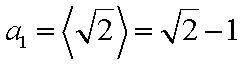
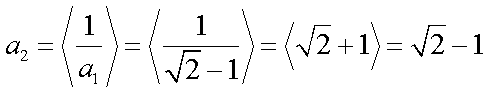
若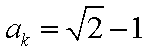
所以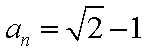
(2)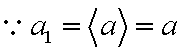
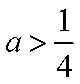
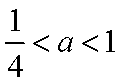
①当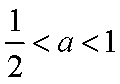
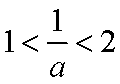
所以
解得:
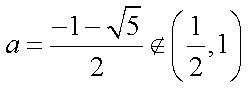
②当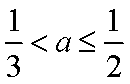
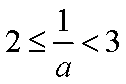
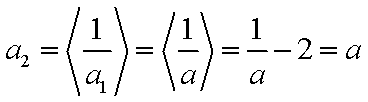
所以
解得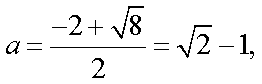

① 当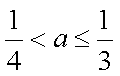
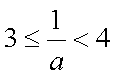
解得
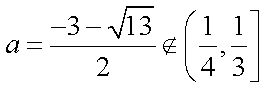
综上,集合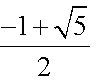
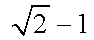
(3)结论成立. 由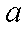
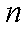
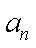
可设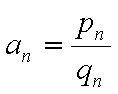
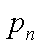
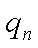
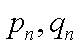
由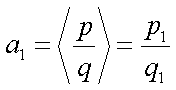
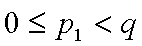
若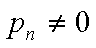
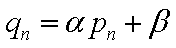

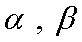
则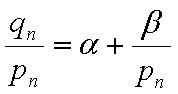
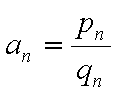
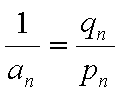
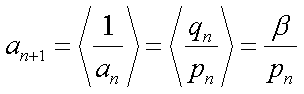
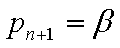
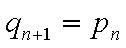
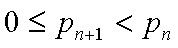
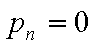
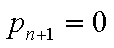
若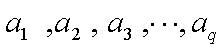
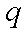
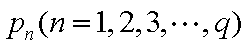
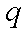
但小于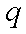
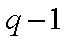
故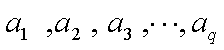

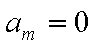
从而数列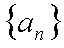
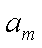
所以对于大于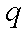
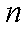
知识点
过点(2,3)且与直线l1:y=0和l2: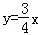
正确答案
42
解析
因为所求圆与y=0相切,所以设圆的圆心坐标(a,r),半径为r,l2: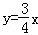
所以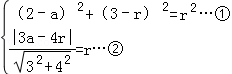
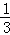
由a=﹣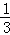
所有半径之和为3+39=42。
由a=3r以及①可得:9r2﹣18r+13=0,因为△=﹣144,方程无解;
综上得,过点(2,3)且与直线l1:y=0和l2: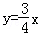
知识点
已知椭圆


(1)求椭圆
(2)设












正确答案
见解析
解析
(1)

(2)设

则

故可设直线
将其与椭圆方程联立,消去


由


同理可得

而
所以
故直线


知识点
扫码查看完整答案与解析